题目内容
9.“a=1”是函数f(x)=1-2sin2(ax+$\frac{π}{4}$)在区间($\frac{π}{12}$,$\frac{π}{6}$)上为减函数“的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 先根据二倍角公式,化简,根据函数的单调性求出a的取值范围,再根据充分条件和必要条件的定义即可判断.
解答 解:f(x)=1-2sin2(ax+$\frac{π}{4}$)=cos(2ax+$\frac{π}{2}$)=-sin2ax,
∵函数f(x)=1-2sin2(ax+$\frac{π}{4}$)在区间($\frac{π}{12}$,$\frac{π}{6}$)上为减函数,
可得a>0,且2a•$\frac{π}{12}$>-$\frac{π}{2}$,2a•$\frac{π}{6}$<$\frac{π}{2}$由此求得a<$\frac{3}{2}$,即实数a的取值范围为(0,$\frac{3}{2}$).
∴“a=1”是函数f(x)=1-2sin2(ax+$\frac{π}{4}$)在区间($\frac{π}{12}$,$\frac{π}{6}$)上为减函数“的充分不必要条件,
故选:A.
点评 本题主要考查正弦函数的单调性,二倍角公式,充分必要条件的判断,属于基础题.

练习册系列答案
相关题目
20.某几何体的三视图如图,其正视图中的曲线部分为半个圆弧,则该几何体的表面积为( )
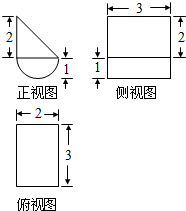

| A. | 16+6$\sqrt{2}$+4π | B. | 16+6$\sqrt{2}$+3π | C. | 10+6$\sqrt{2}$+4π | D. | 10+6$\sqrt{2}$+3π |
4.如图为某几何体的三视图,则该几何体的体积为( )


| A. | 16+π | B. | 16+4π | C. | 8+π | D. | 8+4π |
14.(x2-2)(1+$\frac{2}{x}$)5的展开式中x-1的系数为( )
| A. | 60 | B. | 50 | C. | 40 | D. | 20 |
1.若关于x的方程2x3-3x2+a=0在区间[-2,2]上仅有一个实根,则实数a的取值范围为( )
| A. | (-4,0]∪[1,28) | B. | [-4,28] | C. | [-4,0)∪(1,28] | D. | (-4,28) |
18.一个几何体的三视图如图所示,则该几何体的体积为( )
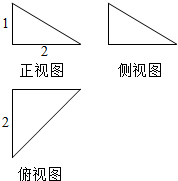

| A. | $\frac{4}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | 2 |