题目内容
3．函数y=lnx（x＞0）的图象与直线$y=\frac{1}{2}x+a$相切，则a等于ln2-1．分析 根据切点在曲线上，可以设切点P（m，lnm），根据导数的几何意义，可以得到切线的斜率a=y′|x=m，再由切点在切线上，可以得到lnm=a+$\frac{1}{2}$m，解两个方程，即可得到a的值．
解答 解：根据切点P在曲线上，
∴设切点P的坐标为（m，lnm），
∵函数y=lnx，
∴y′=$\frac{1}{x}$，
根据导数的几何意义可以得到，切线的斜率k=y′|x=m=$\frac{1}{m}$=$\frac{1}{2}$，①
又切点P（m，lnm）在切线y=$\frac{1}{2}$x+a上，
∴lnm=a+$\frac{1}{2}$m，②
由①②，解得m=2，a=ln2-1，
故答案为：ln2-1．
点评 本题考查了利用导数研究曲线上某点切线方程．导数的几何意义即在某点处的导数即该点处切线的斜率，解题时要注意运用切点在曲线上和切点在切线上．属于中档题．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
13．甲、乙等5人在9月3号参加了纪念抗日战争胜利70周年阅兵庆典后，在天安门广场排成一排拍照留念，甲和乙必须相邻的排法有（ ）种．
| A． | 24 | B． | 48 | C． | 72 | D． | 120 |
14．（x2-2）（1+$\frac{2}{x}$）5的展开式中x-1的系数为（ ）
| A． | 60 | B． | 50 | C． | 40 | D． | 20 |
11．已知正方体ABCD-A′B′C′D′，点E是A′C′的中点，点F是AE的三等分点，且$AF=\frac{1}{2}EF$，则$\overrightarrow{AF}$等于（ ）
| A． | $\overrightarrow{AA′}$+$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ | B． | $\frac{1}{2}$$\overrightarrow{AA′}$+$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ | C． | $\frac{1}{2}$$\overrightarrow{AA′}$+$\frac{1}{6}$$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AD}$ | D． | $\frac{1}{3}$$\overrightarrow{AA′}$+$\frac{1}{6}$$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AD}$ |
18．一个几何体的三视图如图所示，则该几何体的体积为（ ）
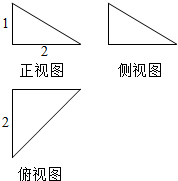
| A． | $\frac{4}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{3}$ | D． | 2 |
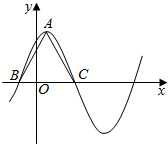函数$f（x）=6{cos^2}\frac{ωx}{2}+\sqrt{3}sinωx-3（{ω＞0}）$在一个周期内的图象如图所示，A为图象的最高点，B、C为图象与x轴的交点，且△ABC为正三角形．
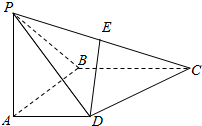如图，在四棱锥P-ABCD中，侧面PAB⊥底面ABCD，且∠PAB=∠ABC=90°，AD∥BC，PA=AB=BC=2AD，E是PC的中点．