题目内容
11．已知命题p：关于x的不等式x2+（a-1）x+1≤0的解集为∅；命题q：方程$\frac{x^2}{2}+\frac{y^2}{a}=1$表示焦点在y轴上的椭圆；若命题?q为真命题，p∨q为真命题．（1）求实数a的取值范围；
（2）判断方程（a+1）x2+（1-a）y2=（a+1）（1-a）所表示的曲线的形状．
分析 （1）若命题?q为真命题，p∨q为真命题．则p为真q为假，进而可得实数a的取值范围；
（2）结合圆锥曲线和圆方程的特点，对a进行分类讨论，可得答案．
解答 解：（1）由题意得 若P为真，则△=（a-1）2-4＜0⇒-1＜a＜3
若q为真，则a＞2；
又命题?q为真命题，p∨q为真命题得，p为真q为假
∴$\left\{{\begin{array}{l}{-1＜a＜3}\\{a≤2}\end{array}}\right.$⇒-1＜a≤2；
（2）由（1）得-1＜a≤2
∴①当a=1时，方程表示一条直线，即y轴；
②当-1＜a＜0时，方程表示焦点在x轴上的椭圆；
③当a=0时，方程表示单位圆；
④当0＜a＜1时，方程表示焦点在y轴上的椭圆；
⑤当1＜a≤2时，方程表示焦点在y轴上的双曲线．
点评 本题以命题的真假判断与应用为载体，考查了复合命题，二次不等式的解法，圆锥曲线的方程，难度中档．
练习册系列答案
相关题目
1．
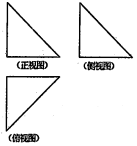如图，一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形，如果直角三角形的斜边长为$\sqrt{2}$，那么这个几何体的体积是（ ）
如图，一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形，如果直角三角形的斜边长为$\sqrt{2}$，那么这个几何体的体积是（ ）| A． | $\frac{{3+\sqrt{3}}}{2}$ | B． | $3+\sqrt{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{3}{2}$ |
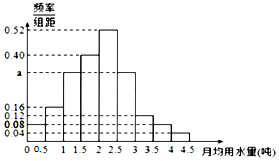我国是世界上严重缺水的国家，某市政府为了鼓励全市30万居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x（吨），一位居民的月用水量不超过x的部分按平价收费，超过x的部分按议价收费，并希望约80%的居民每月的用水量不超过标准x（吨）．为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），[4，4.5）分成9组，制成了如图所示的频率分布直方图．
16．已知集合M={5，log2a}，N={a，b}，若M∩N={1}，则M∪N=（ ）
| A． | {1，2，5} | B． | {0，1，2} | C． | {0，1，5} | D． | {0，2，5} |
1．设函数y=f（x）在x=x0处可导，且$\underset{lim}{△x→0}$$\frac{f（{x}_{0}-3△x）-f（{x}_{0}）}{2△x}$=1，则f′（x0）等于（ ）
| A． | -$\frac{2}{3}$ | B． | -$\frac{3}{2}$ | C． | 1 | D． | -1 |