题目内容
(1)若直线y=-2x+3k+14与直线x-4y=-3k-2的交点位于第四象限,求实数k的取值范围.
(2)由动点P向圆x2+y2=1引两条切线PA、PB,切点分别为A、B,∠APB=60°,求动点P的轨迹方程.
(2)由动点P向圆x2+y2=1引两条切线PA、PB,切点分别为A、B,∠APB=60°,求动点P的轨迹方程.
考点:与直线有关的动点轨迹方程,两条直线的交点坐标
专题:直线与圆
分析:(1)联立方程组,求出交点坐标,利用直线y=-2x+3k+14与直线x-4y=-3k-2的交点位于第四象限,可得不等式,从而可求实数k的取值范围;
(2)设P(x,y),利用∠APB=60°,OA⊥AP,可得|OP|=2|OA|=2,即可求动点P的轨迹方程.
(2)设P(x,y),利用∠APB=60°,OA⊥AP,可得|OP|=2|OA|=2,即可求动点P的轨迹方程.
解答:
解:(1)直线y=-2x+3k+14与直线x-4y=-3k-2,联立方程组,可解得x=k+6,y=k+2
∵直线y=-2x+3k+14与直线x-4y=-3k-2的交点位于第四象限,
∴x=k+6>0,y=k+2<0,
∴-6<k<-2;
(2)解:设P(x,y).
∵∠APB=60°,∴∠OPA=30°.
∵OA⊥AP,∴|OP|=2|OA|=2,
∴
=2,化简得x2+y2=4,
∴动点P的轨迹方程是x2+y2=4.
∵直线y=-2x+3k+14与直线x-4y=-3k-2的交点位于第四象限,
∴x=k+6>0,y=k+2<0,
∴-6<k<-2;
(2)解:设P(x,y).
∵∠APB=60°,∴∠OPA=30°.
∵OA⊥AP,∴|OP|=2|OA|=2,
∴
| x2+y2 |
∴动点P的轨迹方程是x2+y2=4.
点评:本题考查两条直线的交点坐标的求法,考查轨迹方程,考查学生的计算能力,属于中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
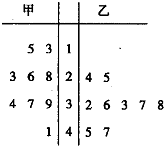 如图是甲、乙两名篮球运动员在以往几场篮球赛中得分的茎叶图,设甲、乙两组数据的平均数分别为
如图是甲、乙两名篮球运动员在以往几场篮球赛中得分的茎叶图,设甲、乙两组数据的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
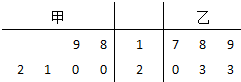 甲、乙两人同时生产一种产品,6天中,完成的产量茎叶图(茎表示十位,叶表示个位)如图所示:
甲、乙两人同时生产一种产品,6天中,完成的产量茎叶图(茎表示十位,叶表示个位)如图所示: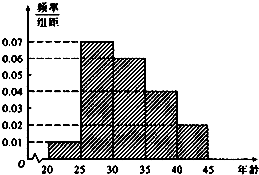 某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.