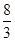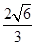题目内容
设 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 为直线
为直线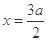 上一点,
上一点,
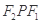 是底角为
是底角为 的等腰三角形,则
的等腰三角形,则 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
C
解析试题分析:∵△F2PF1是底角为30°的等腰三角形,∴|PF2|=|F2F1|∵P为直线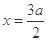 上一点
上一点 ,故选C.
,故选C.
考点:椭圆的几何性质.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
设双曲线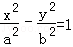 的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为( )
的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为( )
A. | B.5 | C.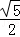 | D.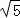 |
过抛物线y 2=4x的焦点作直线,交抛物线于A(x1, y 1) ,B(x2, y 2)两点,如果x1+ x2=6,那么|AB|=
| A.8 | B.10 | C.6 | D.4 |
已知曲线 :
: 和
和 :
: 的焦点分别为
的焦点分别为 、
、 ,点
,点 是
是 和
和 的一个交点,则△
的一个交点,则△ 的形状是( )
的形状是( )
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.都有可能 |
.(5分)直线 与曲线
与曲线 有且只有一个交点,则
有且只有一个交点,则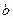 的取值范围是( )
的取值范围是( )
A. | B. 且 且 | C. | D. |
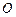 为平面直角坐标系的原点,过点
为平面直角坐标系的原点,过点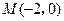 的直线
的直线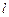 与圆
与圆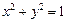 交于
交于 ,
,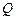 两点.
两点.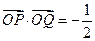 ,求直线
,求直线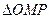 与
与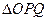 的面积相等,求直线
的面积相等,求直线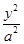 -
-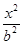 =1(a>0,b>0)的上、下焦点,点F2关于渐近线的对称点恰好
=1(a>0,b>0)的上、下焦点,点F2关于渐近线的对称点恰好

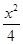 +y2=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF1⊥PF2,则点P的横坐标为( )
+y2=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF1⊥PF2,则点P的横坐标为( )