题目内容
(本小题满分13分)
已知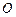 为平面直角坐标系的原点,过点
为平面直角坐标系的原点,过点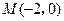 的直线
的直线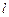 与圆
与圆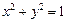 交于
交于 ,
,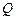 两点.
两点.
(I)若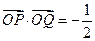 ,求直线
,求直线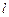 的方程;
的方程;
(Ⅱ)若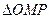 与
与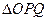 的面积相等,求直线
的面积相等,求直线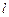 的斜率.
的斜率.
解:(Ⅰ)依题意,直线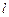 的斜率存在,
的斜率存在,
因为 直线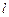 过点
过点 ,可设直线
,可设直线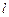 :
: .
.
因为 两点在圆
两点在圆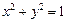 上,所以
上,所以  ,
,
因为 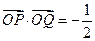 ,所以
,所以  .
.
所以  所以
所以  到直线
到直线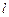 的距离等于
的距离等于 .
.
所以  , 得
, 得 .
.
所以 直线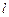 的方程为
的方程为 或
或 . …………6分
. …………6分
(Ⅱ)因为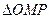 与
与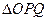 的面积相等,所以
的面积相等,所以 ,
,
设  ,
, ,所以
,所以  ,
, .
.
所以 即
即 (*)
(*)
因为  ,
, 两点在圆上,所以
两点在圆上,所以
把(*)代入得 所以
所以 
故直线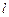 的斜率
的斜率 , 即
, 即 . ………13分
. ………13分
解析

练习册系列答案
相关题目
设 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 为直线
为直线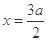 上一点,
上一点,
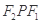 是底角为
是底角为 的等腰三角形,则
的等腰三角形,则 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
 ,
, ).
).
 轴的正半轴建立平面直角坐标系,直线l的参数方程为
轴的正半轴建立平面直角坐标系,直线l的参数方程为 (t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.
(t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积. 中O是坐标原点,
中O是坐标原点, ,圆
,圆 是
是 的外接圆,过点(2,6)的直线为
的外接圆,过点(2,6)的直线为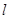 。
。 ,求直线
,求直线 中,
中, 是抛物线
是抛物线
 的焦点,
的焦点, 是抛物线
是抛物线 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过 三点的圆的圆心为
三点的圆的圆心为 ,点
,点 .(Ⅰ)求抛物线
.(Ⅰ)求抛物线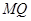 与抛物线
与抛物线 若存在,求出点
若存在,求出点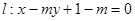
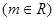 ,圆
,圆 .
.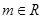 ,直线
,直线 与圆
与圆 恒有两个公共点.
恒有两个公共点.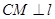 于点
于点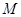 ,当
,当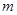 变化时,求点
变化时,求点 的方程.
的方程.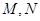 ,与圆
,与圆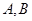 ,是否存在
,是否存在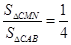 ?若存在,试求出
?若存在,试求出 .
. 向该圆引一条切线,切点为M,O为坐标原点,且有
向该圆引一条切线,切点为M,O为坐标原点,且有 ,
, 取得最小值的点P的坐标
取得最小值的点P的坐标 =a,
=a, =b(a>2,b>2).
=b(a>2,b>2).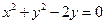 上任一点
上任一点
 的取值范围
的取值范围 恒成立,求实数C的最小值,
恒成立,求实数C的最小值,