题目内容
19.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右顶点分别为A1,A2,点M为椭圆上不同于A1,A2的一点,若直线MA1,MA2与直线的斜率之积为$-\frac{1}{2}$,则椭圆的离心率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 设出M坐标,由直线AM,BM的斜率之积为-$\frac{1}{2}$得一关系式,再由点M在椭圆上变形可得另一关系式,联立后结合隐含条件求得椭圆的离心率.
解答 解:由椭圆方程可知,A(-a,0),B(a,0),
设M(x0,y0),∴${k}_{AM}=\frac{{y}_{0}}{{x}_{0}+a}$,${k}_{BM}=\frac{{y}_{0}}{{x}_{0}-a}$,
则$\frac{{y}_{0}}{{x}_{0}+a}•\frac{{y}_{0}}{{x}_{0}-a}=-\frac{1}{2}$,整理得:$\frac{{{y}_{0}}^{2}}{{{x}_{0}}^{2}-{a}^{2}}=-\frac{1}{2}$,①
又$\frac{{{x}_{0}}^{2}}{{a}^{2}}+\frac{{{y}_{0}}^{2}}{{b}^{2}}=1$,得${{y}_{0}}^{2}=\frac{{b}^{2}}{{a}^{2}}({a}^{2}-{{x}_{0}}^{2})$,
即$\frac{{{y}_{0}}^{2}}{{{x}_{0}}^{2}-{a}^{2}}=-\frac{{b}^{2}}{{a}^{2}}$,②
联立①②,得-$\frac{{b}^{2}}{{a}^{2}}=-\frac{1}{2}$,即$\frac{{a}^{2}-{c}^{2}}{{a}^{2}}=\frac{1}{2}$,解得e=$\frac{\sqrt{2}}{2}$.
故选:C.
点评 本题考查椭圆的简单性质,考查了数学转化思想方法,是中档题.

练习册系列答案
相关题目
9.已知函数f(x)=$\left\{\begin{array}{l}{kx+3,x≥0}\\{(\frac{1}{2})^{x},x<0}\end{array}\right.$,若方程f(f(x))-2=0恰有三个实数根,则实数k的取值范围是( )
| A. | [0,+∞) | B. | [1,3] | C. | (-1,-$\frac{1}{3}$] | D. | [-1,-$\frac{1}{3}$] |
10.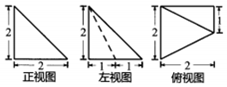 某一空间几何体的三视图如图所示,则该几何体的最长棱长为( )
某一空间几何体的三视图如图所示,则该几何体的最长棱长为( )
 某一空间几何体的三视图如图所示,则该几何体的最长棱长为( )
某一空间几何体的三视图如图所示,则该几何体的最长棱长为( )| A. | 2 | B. | $\sqrt{5}$ | C. | 2$\sqrt{2}$ | D. | 3 |
8.已知复数z满足(1+i)z=1+3i(i是虚数单位),则z的共轭复数为( )
| A. | 1-i | B. | 1+i | C. | 2-i | D. | 2+i |
9.抛物线y2=4x的焦点为F,点A(3,2),P为抛物线上一点,且P不在直线AF上,则△PAF周长的最小值为( )
| A. | 4 | B. | 5 | C. | $4+2\sqrt{2}$ | D. | $5+\sqrt{5}$ |
 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点($\frac{\sqrt{5}}{2}$,$\frac{\sqrt{3}}{2}$),离心率为$\frac{2\sqrt{5}}{5}$,点O位坐标原点.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点($\frac{\sqrt{5}}{2}$,$\frac{\sqrt{3}}{2}$),离心率为$\frac{2\sqrt{5}}{5}$,点O位坐标原点.