��Ŀ����
14�� ��֪��ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������㣨$\frac{\sqrt{5}}{2}$��$\frac{\sqrt{3}}{2}$����������Ϊ$\frac{2\sqrt{5}}{5}$����Oλ����ԭ�㣮
��֪��ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������㣨$\frac{\sqrt{5}}{2}$��$\frac{\sqrt{3}}{2}$����������Ϊ$\frac{2\sqrt{5}}{5}$����Oλ����ԭ�㣮��1������ԲE�ı����̣�
��2������ԲE����F����һ������ֱ���������ֱ��l������ԲE��P��Q���㣬����PQ���е�ΪM����F��PQ���е�ΪM����F��PQ�Ĵ���FN��ֱ��OM�ڵ�N��֤������N��һ����ֱ���ϣ�
���� ��1������Բ�����������a2=5b2�����㣨$\frac{\sqrt{5}}{2}$��$\frac{\sqrt{3}}{2}$��������Բ���̣��������a��b��ֵ��������Բ���̣�
��2����ֱ�߷���l����ֱ��FN��y=-$\frac{1}{k}$��x+2������ֱ��l������Բ���̣�����Τ�ﶨ�����е����깫ʽ������ֱ��OM���̣����ֱ��FN��OM�Ľ���N�����ɵ�֤��
��� �⣺��1���������֪����Բ��������e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{2\sqrt{5}}{5}$��
��a2=5b2��
���㣨$\frac{\sqrt{5}}{2}$��$\frac{\sqrt{3}}{2}$��������Բ$\frac{{x}^{2}}{5{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$����ã�b2=1��a2=5��
����ԲE�ı�����$\frac{{x}^{2}}{5}+{y}^{2}=1$��
��2��֤�����������֪��ֱ��l��б�ʴ��ڣ��Ҳ�Ϊ0��y=k��x+2����ֱ��FN��y=-$\frac{1}{k}$��x+2����
��P��x1��y1����Q��x2��y2����M��x0��y0����
��$\left\{\begin{array}{l}{y=k��x+2��}\\{\frac{{x}^{2}}{5}+{y}^{2}=1}\end{array}\right.$���������1+5k2��x2+20k2x+20k2-5=0��
��Τ�ﶨ����֪��x1+x2=-$\frac{20{k}^{2}}{1+5{k}^{2}}$��x1+x2=$\frac{20{k}^{2}-5}{1+5{k}^{2}}$��
��x0=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{10{k}^{2}}{1+5{k}^{2}}$��y0=k��x0+2��=$\frac{2k}{1+5{k}^{2}}$��
��ֱ��OM��б��ΪkOM=$\frac{{y}_{0}}{{x}_{0}}$=-$\frac{1}{5k}$��
ֱ��OM��y=-$\frac{1}{5k}$x��
$\left\{\begin{array}{l}{y=-\frac{1}{5k}x}\\{y=-\frac{1}{k}��x+2��}\end{array}\right.$����ã�$\left\{\begin{array}{l}{x=-\frac{5}{2}}\\{y=\frac{1}{2k}}\end{array}\right.$��
����kȡ��ֵ��N�ĺ������Ϊ-$\frac{5}{2}$�����N��һ����ֱ��x=-$\frac{5}{2}$�ϣ�
���� ���⿼����Բ�ķ��̵���ע�����������ʹ�ʽ��ע����������ֱ�߷��̺���Բ���̣�����Τ�ﶨ����ͬʱ������ڶ�ֱ���ϵ���ע������ֱ�߷����㣬�������������������е��⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�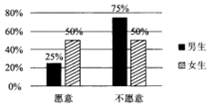 2017��1��1�գ���Ϊ�����д��조ǧ֮�ǡ�27��ʾ���Թ�Ԫ֮һ��Ȫ������ʽ����Ԫ���ڼ䣬Ϊ�˻�Ծ���գ����췽������ˮ����ս��Ŀ��ȫ�����ţ��ִӵ��������������������ȡ��60��������40��Ů����100�˽��е��飬ͳ�Ƴ�100��������Ը�������ս�Ͳ�Ը�������ս����Ů���������������������ͼ����
2017��1��1�գ���Ϊ�����д��조ǧ֮�ǡ�27��ʾ���Թ�Ԫ֮һ��Ȫ������ʽ����Ԫ���ڼ䣬Ϊ�˻�Ծ���գ����췽������ˮ����ս��Ŀ��ȫ�����ţ��ִӵ��������������������ȡ��60��������40��Ů����100�˽��е��飬ͳ�Ƴ�100��������Ը�������ս�Ͳ�Ը�������ս����Ů���������������������ͼ������1�����������������2��2�����������ж��Ƿ��ڷ�����ĸ��ʲ�����1%�������Ը�������ս���Ա��йأ�
| Ը�� | ��Ը�� | �ܼ� | |
| ���� | |||
| �� | |||
| �ܼ� |
�ο���ʽ�����ݣ�
| P��K2��k0�� | 0.1 | 0.05 | 0.025 | 0.01 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
| A�� | ��-�ޣ�1�� | B�� | ��1��+�ޣ� | C�� | ��-�ޣ�2�� | D�� | ��2��+�ޣ� |
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{{\sqrt{2}}}{2}$ | D�� | $\frac{{\sqrt{3}}}{3}$ |
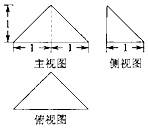
| A�� | 2�� | B�� | 4�� | C�� | 5�� | D�� | 20�� |
| A�� | [-1��6] | B�� | ��1��6] | C�� | [-1��+�ޣ� | D�� | [2��3] |