题目内容
11.设a>0,b>0,若$\sqrt{2}$是4a和2b的等比中项,则$\frac{2}{a}+\frac{1}{b}$的最小值为9.分析 $\sqrt{2}$是4a和2b的等比中项,可得4a•2b=$(\sqrt{2})^{2}$,2a+b=1.再利用“乘1法”与基本不等式的性质即可得出.
解答 解:$\sqrt{2}$是4a和2b的等比中项,∴4a•2b=$(\sqrt{2})^{2}$,∴2a+b=1.
又a>0,b>0,
则$\frac{2}{a}+\frac{1}{b}$=(2a+b)$(\frac{2}{a}+\frac{1}{b})$=5+$\frac{2b}{a}$+$\frac{2a}{b}$≥5+2×$2\sqrt{\frac{b}{a}•\frac{a}{b}}$=9,当且仅当a=b=$\frac{1}{3}$时取等号.
则$\frac{2}{a}+\frac{1}{b}$的最小值为9.
故答案为:9.
点评 本题考查了等比数列的性质、“乘1法”与基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.定义在R上的函数f(x),f′(x)是其导函数,且满足f(x)+f′(x)>2,f(1)=2+$\frac{4}{e}$,则不等式exf(x)>4+2ex的解集为( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,2) | D. | (2,+∞) |
19.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右顶点分别为A1,A2,点M为椭圆上不同于A1,A2的一点,若直线MA1,MA2与直线的斜率之积为$-\frac{1}{2}$,则椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
16.设复数z满足z(2+i)=5i,则|z-1|=( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 5 |
3.某几何体的三视图如图所示,若这个几何体的顶点都在球O的表面上,则球O的表面积是( )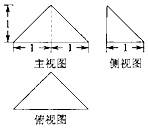

| A. | 2π | B. | 4π | C. | 5π | D. | 20π |
20.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,右顶点为A,过F作AF的垂线与双曲线交于B、C两点,过B作AC的垂线交x轴于点D,若点D到直线BC的距离小于a+$\sqrt{{a}^{2}+{b}^{2}}$,则$\frac{b}{a}$的取值范围为( )
| A. | (0,1) | B. | (1,+∞) | C. | (0,$\sqrt{2}$) | D. | ($\sqrt{2}$,+∞) |
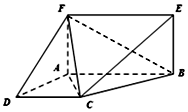 如图,已知AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.
如图,已知AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.