题目内容
10.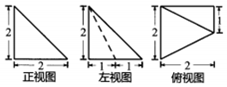 某一空间几何体的三视图如图所示,则该几何体的最长棱长为( )
某一空间几何体的三视图如图所示,则该几何体的最长棱长为( )| A. | 2 | B. | $\sqrt{5}$ | C. | 2$\sqrt{2}$ | D. | 3 |
分析 由三视图知该几何体是底面为直角梯形的直四棱锥,
结合图中数据,即可求出四棱锥中最长的棱长.
解答 解:由三视图知,几何体是一个四棱锥,
且四棱锥的底面是一个直角梯形OABC,
直角梯形的上底是BC=1,下底是AO=2,
垂直于底边的腰是OP=2,
如图所示:
则四棱锥的最长棱长为PB=$\sqrt{{PO}^{2}{+OB}^{2}}$=$\sqrt{{2}^{2}{+2}^{2}{+1}^{2}}$=3.
故选:D.
点评 本题考查了几何体三视图的应用问题,解题的关键是还原出几何体结构特征,是基础题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
20.函数f(x)=x2-4x+4的零点是( )
| A. | (0,2) | B. | (2,0) | C. | 2 | D. | 4 |
5.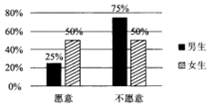 2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
(1)根据条件完成下列2×2列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
(2)水上挑战项目共有两关,主办方规定:挑战过程依次进行,每一关都有两次机会挑战,通过第一关后才有资格参与第二关的挑战,若甲参加每一关的每一次挑战通过的概率均为$\frac{1}{2}$,记甲通过的关数为X,求X的分布列和数学期望.
参考公式与数据:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
 2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:(1)根据条件完成下列2×2列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
| 愿意 | 不愿意 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 |
参考公式与数据:
| P(K2≥k0) | 0.1 | 0.05 | 0.025 | 0.01 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
2.定义在R上的函数f(x),f′(x)是其导函数,且满足f(x)+f′(x)>2,f(1)=2+$\frac{4}{e}$,则不等式exf(x)>4+2ex的解集为( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,2) | D. | (2,+∞) |
19.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右顶点分别为A1,A2,点M为椭圆上不同于A1,A2的一点,若直线MA1,MA2与直线的斜率之积为$-\frac{1}{2}$,则椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
20.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,右顶点为A,过F作AF的垂线与双曲线交于B、C两点,过B作AC的垂线交x轴于点D,若点D到直线BC的距离小于a+$\sqrt{{a}^{2}+{b}^{2}}$,则$\frac{b}{a}$的取值范围为( )
| A. | (0,1) | B. | (1,+∞) | C. | (0,$\sqrt{2}$) | D. | ($\sqrt{2}$,+∞) |
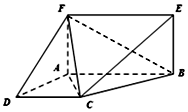 如图,已知AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.
如图,已知AF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4.