题目内容
13.已知点P是平行四边形ABCD所在平面外一点,如果$\overrightarrow{AB}$=(2,-1,-4),$\overrightarrow{AD}$=(4,2,0),$\overrightarrow{AP}$=(-1,2,-1)(1)求证:$\overrightarrow{AP}$是平面ABCD的法向量
(2)求平行四边形ABCD的面积.
分析 (1)由$\overrightarrow{AP}•\overrightarrow{AB}$=0,$\overrightarrow{AP}•\overrightarrow{AD}$=0,得到$\overrightarrow{AP}⊥\overrightarrow{AB}$,$\overrightarrow{AP}⊥\overrightarrow{AD}$,由此能证明$\overrightarrow{AP}$是平面ABCD的法向量.
(2)求出cos<$\overrightarrow{AB},\overrightarrow{AD}$>=$\frac{3\sqrt{105}}{105}$,从而sin∠BAD=$\sqrt{\frac{32}{35}}$,平行四边形ABCD的面积S=|$\overrightarrow{AB}$|•|$\overrightarrow{AD}$|sin∠BAD,由此能求出结果.
解答 证明:(1)∵点P是平行四边形ABCD所在平面外一点,
$\overrightarrow{AB}$=(2,-1,-4),$\overrightarrow{AD}$=(4,2,0),$\overrightarrow{AP}$=(-1,2,-1)
∴$\overrightarrow{AP}•\overrightarrow{AB}$=-2-2+4=0,$\overrightarrow{AP}•\overrightarrow{AD}$=-4+4+0=0,
∴$\overrightarrow{AP}⊥\overrightarrow{AB}$,$\overrightarrow{AP}⊥\overrightarrow{AD}$,
∴AP⊥AB,AP⊥AD,
∵AB∩AD=A,∴AP⊥平面ABCD,
∴$\overrightarrow{AP}$是平面ABCD的法向量.
解:(2)∵|$\overrightarrow{AB}$|=$\sqrt{4+1+16}$=$\sqrt{21}$,
|$\overrightarrow{AD}$|=$\sqrt{16+4+0}$=2$\sqrt{5}$,
∵$\overrightarrow{AB}•\overrightarrow{AD}$=8-2+0=6,
∴cos<$\overrightarrow{AB},\overrightarrow{AD}$>=$\frac{\overrightarrow{AB}•\overrightarrow{AD}}{|\overrightarrow{AB}|•|\overrightarrow{AD}|}$=$\frac{6}{\sqrt{21}×2\sqrt{5}}$=$\frac{3\sqrt{105}}{105}$,
∴sin∠BAD=$\sqrt{1-(\frac{3\sqrt{105}}{105})^{2}}$=$\sqrt{\frac{32}{35}}$,
∴平行四边形ABCD的面积:
S=|$\overrightarrow{AB}$|•|$\overrightarrow{AD}$|sin∠BAD=8$\sqrt{6}$.
点评 本题考查平面的法向量的证明,考查平行四边形的面积的求法,考查平面的法向量、向量余弦夹角公式、同角三角函数关系式等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想、数形结合思想,是中档题.

 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案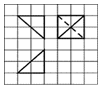 如图所示,网格纸上小正方形的边长为1,粗线画出的是某三棱锥面体的三视图,则该三棱锥的表面积为( )
如图所示,网格纸上小正方形的边长为1,粗线画出的是某三棱锥面体的三视图,则该三棱锥的表面积为( )| A. | 2(1+2$\sqrt{2}$+$\sqrt{3}$) | B. | 2(1+$\sqrt{2}$+$\sqrt{3}$) | C. | $4{+}2\sqrt{6}$ | D. | 4(1+$\sqrt{2}$) |
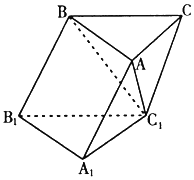 如图,在斜三棱柱中ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,点P为AC1上的一个动点,则点P在底面ABC上的射影H必在( )
如图,在斜三棱柱中ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,点P为AC1上的一个动点,则点P在底面ABC上的射影H必在( )| A. | 直线AB上 | B. | 直线BC上 | C. | 直线AC上 | D. | △ABC内部 |
| A. | b<a<c | B. | c<b<a | C. | b<c<a | D. | a<b<c |
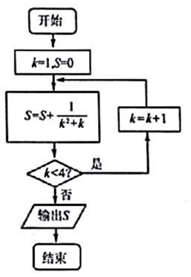
| A. | $\frac{5}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{5}{6}$ |
| A. | $({\frac{4}{5},16})$ | B. | $({\frac{{2\sqrt{5}}}{5},16})$ | C. | (1,16) | D. | (1,4) |
 如图,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB,AD,CB,CD上,分别截取AE=AH=CF=CG=x(x>0),设四边形EFGH的面积为y.
如图,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB,AD,CB,CD上,分别截取AE=AH=CF=CG=x(x>0),设四边形EFGH的面积为y. 如图是某学校某年级的三个班在一学期内的六次数学测试的平均成绩y关于测试序号x的函数图象,为了容易看出一个班级的成绩变化,将离散的点用虚线连接,根据图象,给出下列结论:
如图是某学校某年级的三个班在一学期内的六次数学测试的平均成绩y关于测试序号x的函数图象,为了容易看出一个班级的成绩变化,将离散的点用虚线连接,根据图象,给出下列结论: