题目内容
9.集合A={x|-1<x<1},B={x|x<a}.(1)若A∩B=∅,求a的取值范围;
(2)若A∪B={x|x<1},求a的取值范围.
分析 (1)由A={x|-1<x<1},B={x|x<a},且A∩B=∅,作出数轴,由数轴上的点x=a在x=-1的左侧(含点x=-1),能求出a的取值范围.
(2)由A={x|-1<x<1},B={x|x<a},且A∪B={x|x<1},知数轴上的点x=a在x=-1和x=1之间(含点x=1,但不含点x=-1),由此能求出a的取值范围.
解答 解:(1)如下图所示,A={x|-1<x<1},B={x|x<a},且A∩B=∅,
∴数轴上的点x=a在x=-1的左侧(含点x=-1),
∴a≤-1,即a的取值范围为{a|a≤-1}.
(2)如下图所示,A={x|-1<x<1},B={x|x<a},且A∪B={x|x<1},
∴数轴上的点x=a在x=-1和x=1之间(含点x=1,但不含点x=-1),
∴-1<a≤1,即a的取值范围为{a|-1<a≤1}.
点评 本题考查实数的取值范围的求法,考查集合、交集等基础知识,是基础题,解题时要认真审题,注意交集性质的合理运用.

练习册系列答案
相关题目
20.已知一组数据3、4、5、s、t的平均数是4,中位数是m,对于任意实数s、t,从3、4、5、s、t、m这组数据中任取一个,取到数字4的概率的最大值为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
1.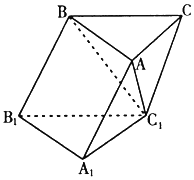 如图,在斜三棱柱中ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,点P为AC1上的一个动点,则点P在底面ABC上的射影H必在( )
如图,在斜三棱柱中ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,点P为AC1上的一个动点,则点P在底面ABC上的射影H必在( )
 如图,在斜三棱柱中ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,点P为AC1上的一个动点,则点P在底面ABC上的射影H必在( )
如图,在斜三棱柱中ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,点P为AC1上的一个动点,则点P在底面ABC上的射影H必在( )| A. | 直线AB上 | B. | 直线BC上 | C. | 直线AC上 | D. | △ABC内部 |
18.如果执行如图的框图,则输出的数S=( )
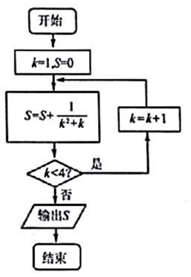

| A. | $\frac{5}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{5}{6}$ |
12.已知ξ的分布列为:
则Eξ等于( )
| ξ | 1 | 2 | 3 | 4 |
| P | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{4}$ |
| A. | $\frac{29}{12}$ | B. | $\frac{131}{144}$ | C. | $\frac{11}{144}$ | D. | $\frac{179}{144}$ |
 如图,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB,AD,CB,CD上,分别截取AE=AH=CF=CG=x(x>0),设四边形EFGH的面积为y.
如图,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB,AD,CB,CD上,分别截取AE=AH=CF=CG=x(x>0),设四边形EFGH的面积为y.