题目内容
4.用秦九韶算法计算多项式f(x)=3x5+2x3-8x+5在x=2时的值时,V4的值为48.分析 由于函数f(x)=3x5+2x3-8x+5=((((3x+0)x+2)x+0)x-8)x+5.
当x=2时,按照从内到外的顺序,依次计算一次多项式当x=2时的值.v0=3;v1=v0×2+0=3×2+0=6;v2=v1×2+2=6×2+2=14;v3=v2×2+0=14×2+0=28;v4=v3×2-8=28×2-8=48;即可得出.
解答 解:函数f(x)=3x5+2x3-8x+5=((((3x+0)x+2)x+0)x-8)x+5.
当x=2时,
v0=3;
v1=v0×2+0=3×2+0=6;
v2=v1×2+2=6×2+2=14;
v3=v2×2+0=14×2+0=28;
v4=v3×2-8=28×2-8=48
故答案为:48.
点评 本题考查了秦九韶算法计算函数值,考查了计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.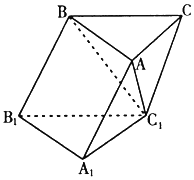 如图,在斜三棱柱中ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,点P为AC1上的一个动点,则点P在底面ABC上的射影H必在( )
如图,在斜三棱柱中ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,点P为AC1上的一个动点,则点P在底面ABC上的射影H必在( )
 如图,在斜三棱柱中ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,点P为AC1上的一个动点,则点P在底面ABC上的射影H必在( )
如图,在斜三棱柱中ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,点P为AC1上的一个动点,则点P在底面ABC上的射影H必在( )| A. | 直线AB上 | B. | 直线BC上 | C. | 直线AC上 | D. | △ABC内部 |
12.已知ξ的分布列为:
则Eξ等于( )
| ξ | 1 | 2 | 3 | 4 |
| P | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{4}$ |
| A. | $\frac{29}{12}$ | B. | $\frac{131}{144}$ | C. | $\frac{11}{144}$ | D. | $\frac{179}{144}$ |
19.若集合A={x||2x|>1},B={x|2x2-x-1<0},则A∩B=( )
| A. | {x|-1<x<2} | B. | $\left\{{x\left|{\frac{1}{2}<x<1}\right.}\right\}$ | C. | $\left\{{x\left|{-\frac{1}{2}<x<1}\right.}\right\}$ | D. | {x|x>1} |
16.已知正实数x,y满足2<2x+y<4,则x2+y2的取值范围是( )
| A. | $({\frac{4}{5},16})$ | B. | $({\frac{{2\sqrt{5}}}{5},16})$ | C. | (1,16) | D. | (1,4) |
 如图是某学校某年级的三个班在一学期内的六次数学测试的平均成绩y关于测试序号x的函数图象,为了容易看出一个班级的成绩变化,将离散的点用虚线连接,根据图象,给出下列结论:
如图是某学校某年级的三个班在一学期内的六次数学测试的平均成绩y关于测试序号x的函数图象,为了容易看出一个班级的成绩变化,将离散的点用虚线连接,根据图象,给出下列结论: 已知正方体ABCD-A1B1C1D1中,E是BB1的中点
已知正方体ABCD-A1B1C1D1中,E是BB1的中点