题目内容
已知:x>y>0,且xy=1,若x2+y2≥a(x-y)恒成立,则a的取值范围为 .
考点:函数恒成立问题
专题:转化思想,不等式的解法及应用
分析:由已知把x2+y2≥a(x-y)恒成立转化为a≤
恒成立,整理后代入xy=1,然后利用基本不等式求最值,从而得到a的取值范围.
| x2+y2 |
| x-y |
解答:
解:∵x>y>0,
由x2+y2≥a(x-y)恒成立,得a≤
恒成立,
又
=
,
而x>y>0,且xy=1,
∴
=
=
=(x-y)+
≥2
=2
,
∴a≤2
.
故答案为a≤2
.
由x2+y2≥a(x-y)恒成立,得a≤
| x2+y2 |
| x-y |
又
| x2+y2 |
| x-y |
| (x-y)2+2xy |
| x-y |
而x>y>0,且xy=1,
∴
| x2+y2 |
| x-y |
| (x-y)2+2xy |
| x-y |
| (x-y)2+2 |
| x-y |
| 2 |
| x-y |
(x-y)•
|
| 2 |
∴a≤2
| 2 |
故答案为a≤2
| 2 |
点评:本题考查了函数恒成立问题,考查了数学转化思想方法,训练了基本不等式求最值,是中档题.

练习册系列答案
相关题目
抛物线y2=4x的焦点为F,点A,B在抛物线上,且∠AFB=120°,弦AB中点M在其准线上的射影为N,则
的最大值为( )
| |MN| |
| |AB| |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
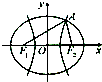 如图,F1,F2是双曲线C1:x2-
如图,F1,F2是双曲线C1:x2-