题目内容
17．体积为$\frac{4}{3}π$的球O放置在棱长为4的正方体ABCD-A1B1C1D1上，且与上表面A1B1C1D1相切，切点为该表面的中心，则四棱锥O-ABCD的外接球的半径为$\frac{33}{10}$．分析 体积为$\frac{4}{3}$π的球O的半径为1，四棱锥O-ABCD的底面边长为4，高为5，设四棱锥O-ABCD的外接球的半径为R，利用勾股定理，建立方程，即可求出四棱锥O-ABCD的外接球的半径．
解答 解：体积为$\frac{4}{3}π$的球O的半径为1，四棱锥O-ABCD的底面边长为4，高为5，
设四棱锥O-ABCD的外接球的半径为R，则R2=（5-R）2+（2$\sqrt{2}$）2，
∴R=$\frac{33}{10}$．
故答案为$\frac{33}{10}$．
点评 本题考查球的体积的计算，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
6．已知几何体的三视图如图所示，则该几何体的体积为（ ）
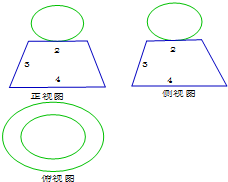
| A． | $\frac{π}{3}（4+14\sqrt{2}）$ | B． | $\frac{{14\sqrt{2}π}}{3}$ | C． | $\frac{5π}{3}$ | D． | $\frac{4π}{3}$ |
如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AB⊥AD，AB∥CD，$CD=2AB=2BP=\sqrt{2}AD$，$\overrightarrow{CE}=λ\overrightarrow{EB}$（λ＞0），DE⊥平面PBC，侧面ABP⊥底面ABCD
5．根据国家最新人口发展战略，一对夫妇可生育两个孩子，为了解人们对放开生育二胎政策的意向，某机构在A城市随机调查了100位30到40岁已婚人群，得到情况如表：
（Ⅰ）是否有95%以上的把握认为“生二胎与性别有关”，并说明理由（请参考所附的公式及相关数据）；
（Ⅱ）从这60名男性中按对生育二胎政策的意向采取分层抽样，抽取6名男性，从这6名男性中随机选取两名，求选到的两名都愿意生育二胎的概率．
K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| 意向 | 男 | 女 | 合计 |
| 生 | 40 | 20 | 60 |
| 不生 | 20 | 20 | 40 |
| 合计 | 60 | 40 | 100 |
（Ⅱ）从这60名男性中按对生育二胎政策的意向采取分层抽样，抽取6名男性，从这6名男性中随机选取两名，求选到的两名都愿意生育二胎的概率．
K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| P（K2≥k） | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |