题目内容

棱长为1的正方体ABCD-A1B1C1D1中，P，M分别为线段BD1，B1C1上的点，若BP=2PD1，则三棱锥M-PBC的体积．
考点：棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：利用直线与平面平行，转化所求几何体的体积为同底面高相等的棱锥的体积，即可求出三棱锥M-PBC的体积．
解答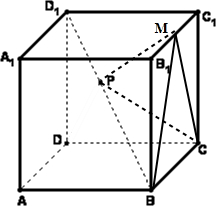： 解：∵棱长为3的正方体ABCD-A1B1C1D1中，
P、M分别为线段BD1，B1C1上的点，BP=2PD1，因为几何体是正方体，所以B1M∥BC，
∴M到面PBC的距离与B1到面PBC的距离相等，三棱锥M-PBC的体积
转化为：三棱锥P-B1BC的体积，正方体的棱长为1，
BP=2PD1，P到平面B1BC的距离为：
2
3
，
∴VM-PBC=VP-BB1C=
1
3
×
1
2
×1×1×
2
3
=
1
9
．
点评：本题考查三棱锥的体积的求法，解题时要认真审题，仔细解答，注意合理地化空间问题为平面问题，考查转化思想的应用．
练习册系列答案
相关题目
已知函数f（x）=x2-（m+2）x-m+1有两个零点，则m的取值范围是
 
（用区间表示）
若θ∈（
π
2
，π），
a
=（1，sinθ），
b
=（3sinθ，1），且
a
∥
b
，则cos（θ+
π
6
）=
 
．
对于实数m，n定义运算“⊕”：m⊕n=
-m2+2mn-1，m≤n
n2-mn，m＞n
，设f（x）=（2x-1）⊕（x-1），且关于x的方程f（x）=a恰有三个互不相等的实数根x1，x2，x3，则x1x2x3的取值范围是（　　）
A、（-
1
32
，0）
B、（-
1
16
，0）
C、（0，
1
32
）
D、（0，
1
16
）
已知函数f（x）=x3+3ax2+3bx+c在x=2处有极值，其图象在x=1处的切线与直线6x+2y+5=0平行．
（Ⅰ）求a，b的值和函数f（x）的单调区间；
（Ⅱ）当x∈[1，3]时，f（x）＞1-4c2恒成立，求实数c的取值范围．
如图，PA、PB分别切⊙O于点 A、B，点C在⊙O的劣弧AB上，且∠ACB=130°，则∠P=
 
．
等差数列{an}中，a1=1，a2=3，数列{
1
anan+1
}的前n项和为
15
31
，则n的值为
 
．
已知函数f（x）=sin（2wx-
π
6
）-4sin2wx+2（w＞0），其图象与x轴相邻两个交点的距离为
π
2
．
（1）求函数f（x）的解析式；
（2）若将f（x）的图象向左平移m（m＞0）个长度单位得到函数g（x）的图象恰好经过点（-
π
3
，0），求当m取得最小值时，g（x）在[-
π
6
，
7π
12
]上的单调增区间．
若P是长度为6的线段AB上任意一点，则点P到线段AB两端距离均不小于1的概率（　　）
A、
5
6
B、
2
3
C、
1
2
D、
1
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网