题目内容
如图，PA、PB分别切⊙O于点 A、B，点C在⊙O的劣弧AB上，且∠ACB=130°，则∠P= ．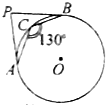
考点：与圆有关的比例线段
专题：选作题,立体几何
分析：连接OA，OB，利用圆周角定理得到∠AOB=130°，然后在四边形AOBP中求出∠P的度数．
解答：
解：连接OA，OB，
∵∠ACB=130°，
∴∠AOB=100°，
∵PA，PB是⊙O的切线，
∴∠PAO=∠PBO=90°，
∴∠P=360°-90°-90°-100°=80°．
故答案是：80°．
∵∠ACB=130°，
∴∠AOB=100°，
∵PA，PB是⊙O的切线，
∴∠PAO=∠PBO=90°，
∴∠P=360°-90°-90°-100°=80°．
故答案是：80°．
点评：本题考查的是切线的性质，利用切线的性质和圆周角定理求出角的度数．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知函数f（x）=2x3-3ax2+8，若f（x）存在唯一的零点x0，且x0＜0，则实数a的取值范围是（ ）
| A、（-∞，0） |
| B、（-∞，0）∪[2，+∞） |
| C、[0，2] |
| D、（-∞，2） |
集合A={x|y=
}，B={y|y=log2x，x＞0}，则A∩B等于（ ）
| x |
| A、R | B、∅ |
| C、[0，+∞） | D、（0，+∞） |
已知函数f（x）=xcos
，存在f（x）的零点x0，（x0≠0），满足[f′（x0）]2＜π2（λ2-x02），则λ的取值范围是（ ）
| πx |
| λ |
A、（-
| ||||||||
B、（-
| ||||||||
C、（-∞，-
| ||||||||
D、（-∞，-
|