题目内容
已知等差数列{an}的前m项的和是25，前2m项的和是100，则前3m项的和是 ．
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：数列{an}是等差数列，Sm，S2m-Sm，S3m-S2m成等差数列，即可求解．
解答：
解：∵数列{an}是等差数列，
∴Sm，S2m-Sm，S3m-S2m成等差数列，
∵等差数列{an}的前m项的和是25，前2m项的和是100，
∴25，100-25，S3m-100成等差数列，
∴2（100-25）=25+S3m-100，
∴S3m=225．
故答案为：225．
∴Sm，S2m-Sm，S3m-S2m成等差数列，
∵等差数列{an}的前m项的和是25，前2m项的和是100，
∴25，100-25，S3m-100成等差数列，
∴2（100-25）=25+S3m-100，
∴S3m=225．
故答案为：225．
点评：利用数列{an}是等差数列，Sm，S2m-Sm，S3m-S2m成等差数列是解题的关键．
练习册系列答案
相关题目
如图所示的圆盘由八个全等的扇形构成，指针绕中心旋转，可能随机停止则指针停止在阴影部分内的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
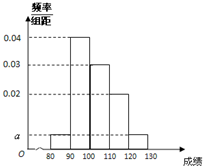为了分析我校市二模文科数学的成绩，现抽样统计了20位同学的数学成绩，形成了如图所示的频率分布直方图，其中成绩的分组区间是：[80，90），[90，100），[100，110），[110，120），[120，130]