题目内容
若z=
|z|+i2015(i为虚数单位),则复数z对应的点位于( )
| 1 |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:复数的代数表示法及其几何意义
专题:计算题,数系的扩充和复数
分析:z=
|z|+i2015可化为z=
|z|-i,设z=a+bi(a,b∈R),则a+bi=
-i,由复数相等的条件可求a、b,进而由几何意义可得答案.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a2+b2 |
解答:
解:z=
|z|+i2015可化为z=
|z|-i,
设z=a+bi(a,b∈R),
则a+bi=
-i,
∴
,解得
,
∴z=
-i对应点为(
,-1),位于第四象限,
故选D.
| 1 |
| 2 |
| 1 |
| 2 |
设z=a+bi(a,b∈R),
则a+bi=
| 1 |
| 2 |
| a2+b2 |
∴
|
|
∴z=
| ||
| 3 |
| ||
| 3 |
故选D.
点评:该题考查复数代数形式的运算法则、复数的几何意义,属基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
曲线y=2x2在点(1,2)处的瞬时变化率为( )
| A、2 | B、4 | C、5 | D、6 |
| 1 |
| i |
| A、1 | B、i | C、-i | D、-1 |
已知sin(
+α)=
,则cos(α-
)=( )
| π |
| 6 |
| 1 |
| 3 |
| π |
| 3 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
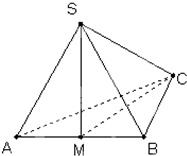 如图,在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2
如图,在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2