题目内容
下列函数是在（0，1）上为减函数的是（ ）
| A、y=x2 |
| B、y=x+1 |
| C、y=sinx |
| D、y=cosx |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：首先，根据条件：在（0，1）上为减函数，逐个选项判断即可．
解答：
解：对于选项A：
函数y=x2在（0，1）上为增函数，
不合乎题意，
对于选项B：
函数y=x+1在（0，1）上为增函数，
不合乎题意，
对于选项C：
函数y=sinx在（0，1）上为增函数，
不合乎题意，
只有选项D符合题意，
故选：D．
函数y=x2在（0，1）上为增函数，
不合乎题意，
对于选项B：
函数y=x+1在（0，1）上为增函数，
不合乎题意，
对于选项C：
函数y=sinx在（0，1）上为增函数，
不合乎题意，
只有选项D符合题意，
故选：D．
点评：本题重点考查了函数的单调性，常见函数的单调性是考查的重点，也是近几年高考考查的热点问题，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
由“正三角形的内切圆切于三边的中点”，可类比猜想出正四面体的内切球切于四个侧面三角形 （ ）
| A、内任一点 | B、某高线上的点 |
| C、中心 | D、外的某点 |
下列各组函数中，表示同一函数的是（ ）
A、y=x与y=
| ||||||
B、y=
| ||||||
| C、y=4lgx与y=2lgx2 | ||||||
D、y=-2+lgx与y=lg
|
函数f（x）=2sin（
x+
）是（ ）
| 2 |
| 3 |
| 15π |
| 2 |
| A、周期为3π的偶函数 | ||
| B、周期为3π的奇函数 | ||
C、周期为
| ||
D、周期为
|
东北育才双语学校门口东侧连续并排共有10个停车位，如果6辆私家车停完后剩余的4个空车位正好在一起的停法种数是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
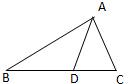如图，已知| AB |
| a |
| AC |
| b |
| BD |
| DC |
| a |
| b |
| AD |
| AD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
函数f（x）=2lnx-
x2+x的图象大致是（ ）
| 1 |
| 2 |
A、 |
B、 |
C、 |
D、 |
已知偶函数f（x）在区间[0，4]上是增函数，则f（-3）和f（π）的大小关系是（ ）
| A、f（-3）＞f（π） |
| B、f（-3）≥f（π） |
| C、f（-3）＜f（π） |
| D、无法确定 |
在三角形ABC中，如果a2+c2-b2=ac，那么B等于（ ）
| A、30° | B、60° |
| C、120° | D、150° |