题目内容
由“正三角形的内切圆切于三边的中点”，可类比猜想出正四面体的内切球切于四个侧面三角形 （ ）
| A、内任一点 | B、某高线上的点 |
| C、中心 | D、外的某点 |
考点：类比推理
专题：常规题型,空间位置关系与距离
分析：给出的是面上线的中点，则类比时，体内面的“中点”，称为中心．
解答：
解：正四面体的内切球切于四个侧面三角形的中心．
故选C．
故选C．
点评：本题考查了类比推理，注意推理要作适当的变换．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
若a、b、c、d、x、y 是正实数，且P=
+
，Q=
•
，则（ ）
| ab |
| cd |
| ax+cy |
|
| A、P=Q |
| B、P3=Q |
| C、P≥Q |
| D、P＞Q |
函数f（x）=
的定义域为（ ）
| lnx+1 | ||
|
| A、（-1，+∞） |
| B、（-∞，1） |
| C、（0，1） |
| D、（-1，1] |
下列函数幂函数有（ ）个．
y=2x2；y=x2；y=x2+x；y=
．
y=2x2；y=x2；y=x2+x；y=
| 1 |
| x2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
f（x）=x3+bx2+cx+d的导函数f′（x）的图象关于直线x=2对称，则b的值为（ ）
| A、-3 | B、3 | C、1 | D、-6 |
下列函数中，周期为π的函数是（ ）
A、y=sin
| ||
| B、y=|sinx| | ||
| C、y=sinx+|sinx| | ||
D、y=|sinx+
|
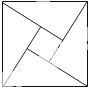2002年8月，在北京召开的国际数学家大会会标如图所示，会标是以我国古代数学家赵爽的弦图为基础设计的．弦图是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形，若直角三角形中较小的锐角为θ，大正方形的面积是1，小正方形的面积是| 1 |
| 25 |
| A、1 | ||
B、-
| ||
C、
| ||
D、-
|
下列函数是在（0，1）上为减函数的是（ ）
| A、y=x2 |
| B、y=x+1 |
| C、y=sinx |
| D、y=cosx |