题目内容
下列各组函数中,表示同一函数的是( )
A、y=x与y=
| ||||||
B、y=
| ||||||
| C、y=4lgx与y=2lgx2 | ||||||
D、y=-2+lgx与y=lg
|
考点:判断两个函数是否为同一函数
专题:函数的性质及应用
分析:首先,逐个进行求解函数的定义域和对应关系,然后,判断是否为同一函数.
解答:
解:选项A:
函数y=
=|x|,
它们对应关系不同,
∴不是同一函数;
对于选项B:
函数y=
的定义域为
(-∞,1)∪(1,+∞),
它们定义域不同,
∴不是同一函数;
选项C:
函数y=4lgx的定义域为(0,+∞),
函数y=2lgx2的定义域为(-∞,0)∪(0,+∞),
∴不是同一函数;
只有选项D符合条件,
故选:D.
函数y=
| x2 |
它们对应关系不同,
∴不是同一函数;
对于选项B:
函数y=
| x-1 | ||
|
(-∞,1)∪(1,+∞),
它们定义域不同,
∴不是同一函数;
选项C:
函数y=4lgx的定义域为(0,+∞),
函数y=2lgx2的定义域为(-∞,0)∪(0,+∞),
∴不是同一函数;
只有选项D符合条件,
故选:D.
点评:本题重点考查了函数的定义域和对应关系、函数是否为同一函数的判断等知识,属于对基础知识的考查范畴,也是近几年高考常考题型,需要引起高度重视.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
若a、b、c、d、x、y 是正实数,且P=
+
,Q=
•
,则( )
| ab |
| cd |
| ax+cy |
|
| A、P=Q |
| B、P3=Q |
| C、P≥Q |
| D、P>Q |
下列函数中,周期为π的函数是( )
A、y=sin
| ||
| B、y=|sinx| | ||
| C、y=sinx+|sinx| | ||
D、y=|sinx+
|
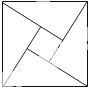 2002年8月,在北京召开的国际数学家大会会标如图所示,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是
2002年8月,在北京召开的国际数学家大会会标如图所示,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是| 1 |
| 25 |
| A、1 | ||
B、-
| ||
C、
| ||
D、-
|
幂函数y=xm与y=xn在第一象限内的图象如图所示,则( )


| A、-1<n<0,<m<1 |
| B、n<-1,0<m<1 |
| C、-1<n<0,m>1 |
| D、n<-1,m>1 |
函数y=cosωx(ω>0)在区间[0,1)上至少出现2次最大值,至多出现3次最大值,则ω的取值范围是( )
| A、2π≤ω≤4π |
| B、2π<ω≤4π |
| C、2π<ω≤6π |
| D、2π<ω<6π |
设(x,y)在映射f下的象是(x+y,x-y),则象(1,2)的原象是( )
| A、(3,1) | ||||
B、(
| ||||
| C、(-1,3) | ||||
D、(-
|
下列函数是在(0,1)上为减函数的是( )
| A、y=x2 |
| B、y=x+1 |
| C、y=sinx |
| D、y=cosx |
i为虚数单位,则(1+i)(1-i)=( )
| A、2i | B、-2i | C、2 | D、-2 |