题目内容
如图,在正四面体S-ABC中,E,F,G,H分别是棱SB,SA,AC,CB的中点.
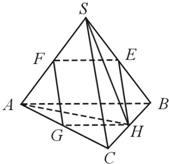
(1)求证:四边形EFGH是平行四边形;
(2)求证:SC∥平面EFGH;
(3)求证:BC⊥平面SAH.

(1)求证:四边形EFGH是平行四边形;
(2)求证:SC∥平面EFGH;
(3)求证:BC⊥平面SAH.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)∵E,F,G,H分别是棱SB,SA,AC,CB的中点,利用中位线的性质得证;
(2)由(1)知,FG∥SC,利用线面平行的判定定理可得;
(3)∵S-ABC是正四面体,所以它的四个面是全等的等边三角形,H是BC的中点,得到BC⊥SH,BC⊥AH,由线面垂直的判定定理可证.
(2)由(1)知,FG∥SC,利用线面平行的判定定理可得;
(3)∵S-ABC是正四面体,所以它的四个面是全等的等边三角形,H是BC的中点,得到BC⊥SH,BC⊥AH,由线面垂直的判定定理可证.
解答:
证明:(1)∵E,F,G,H分别是棱SB,SA,AC,CB的中点,
∴FG∥SC,EH∥SC,且FG=
SC,EH=
SC,(2分)
∴FG∥EH且FG=EH,(3分)
∴四边形EFGH是平行四边形.(4分)
(2)由(1)知,FG∥SC,(5分)
且FG?平面EFGH,SC?平面EFGH,(7分)
∴SC∥平面EFGH.(8分)
(3)∵S-ABC是正四面体,
所以它的四个面是全等的等边三角形.(9分)
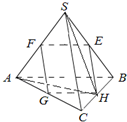
∵H是BC的中点,
∴BC⊥SH,BC⊥AH.(11分)
又SH?平面SAH,AH?平面SAH,且SH∩AH=H,(12分)
∴BC⊥平面SAH.(13分)
∴FG∥SC,EH∥SC,且FG=
| 1 |
| 2 |
| 1 |
| 2 |
∴FG∥EH且FG=EH,(3分)
∴四边形EFGH是平行四边形.(4分)
(2)由(1)知,FG∥SC,(5分)
且FG?平面EFGH,SC?平面EFGH,(7分)
∴SC∥平面EFGH.(8分)
(3)∵S-ABC是正四面体,
所以它的四个面是全等的等边三角形.(9分)

∵H是BC的中点,
∴BC⊥SH,BC⊥AH.(11分)
又SH?平面SAH,AH?平面SAH,且SH∩AH=H,(12分)
∴BC⊥平面SAH.(13分)
点评:本题考查了三角形中位线的性质、线面平行、线面垂直的判定定理的运用,熟练运用判定定理是证明的关键,属于基础题

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
在区间[-5,5]内随机取出一个实数a,则a∈(0,1)的概率为( )
| A、0.5 | B、0.3 |
| C、0.2 | D、0.1 |
某人午觉醒来,发现表停了,他打开收音机,想听电台报时,则他等待的时间不超过10分钟的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设a,b表示两条直线,α,β表示两个平面,下列命题中正确的是( )
| A、a∥b,b?α,则a∥α |
| B、a∥α,a?β,α∩β=b,则a∥b |
| C、α∥β,a?α,b?β,则a∥b |
| D、a∥α,b∥α,则a∥b |
下列函数为偶函数的是( )
| A、y=sinx | ||
B、y=ln(
| ||
| C、y=ex | ||
D、y=ln
|
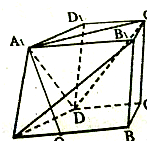 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是一个直角梯形,AB∥CD,∠ABC=90°.CD=3,BC=2,AB=5,AA1=2
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是一个直角梯形,AB∥CD,∠ABC=90°.CD=3,BC=2,AB=5,AA1=2