题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且bcosC=(3a-c)cosB.
(1)求sinB的值;
(2)若b=2,且a=c,求△ABC的面积.
(1)求sinB的值;
(2)若b=2,且a=c,求△ABC的面积.
考点:正弦定理,余弦定理
专题:计算题,解三角形
分析:(1)由已知化简可得sinA=3sinAcosB,即可求得sinB的值;
(2)由(1)得cosB=
,从而可由余弦定理解得a2的值,从而可求△ABC的面积.
(2)由(1)得cosB=
| 1 |
| 3 |
解答:
解:(1)∵已知bcosC=(3a-c)cosB.
∴由正弦定理可得:sinBcosC=(3sinA-sinC)cosB,
即有sinBcosC+sinCcosB=3sinAcosB,
∴sin(B+C)=sinA=3sinAcosB,
∵A为△ABC的内角,有sinA≠0,两边同时除以sinA,可解得cosB=
,
∴sinB=
.
(2)∵由余弦定理可得:b2=a2+c2-2accosB,…①
又∵已知b=2,a=c,由(1)知cosB=
∴由①可得:4=a2+a2-2a2×
,从而解得:a2=3
∴S=
acsinB=
a2sinB=
.
∴由正弦定理可得:sinBcosC=(3sinA-sinC)cosB,
即有sinBcosC+sinCcosB=3sinAcosB,
∴sin(B+C)=sinA=3sinAcosB,
∵A为△ABC的内角,有sinA≠0,两边同时除以sinA,可解得cosB=
| 1 |
| 3 |
∴sinB=
2
| ||
| 3 |
(2)∵由余弦定理可得:b2=a2+c2-2accosB,…①
又∵已知b=2,a=c,由(1)知cosB=
| 1 |
| 3 |
∴由①可得:4=a2+a2-2a2×
| 1 |
| 3 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
点评:本题主要考察了正弦定理、余弦定理的综合应用,属于基础题.

练习册系列答案
相关题目
湖面上飘着一个小球,湖水结冰后将球取出,冰面上留下一个半径为6cm,深2cm的空穴,则取出该球前,球面上的点到冰面的最大距离为( )
| A、20cm | B、18cm |
| C、10cm | D、8cm |
设某产品2013年12月底价格为a元(a>0),在2014年的前6个月,价格平均每月比上个月上涨10%,后6个月,价格平均每月比上个月下降10%,经过这12个月,2014年12月底该产品的价格为b元,则a,b的大小关系是( )
| A、a>b | B、a<b |
| C、a=b | D、不能确定 |
已知
,
,
表示共面的三个单位向量,
⊥
,那么(
+
)•(
+
)的取值范围是( )
| i |
| j |
| k |
| i |
| j |
| i |
| k |
| j |
| k |
| A、[-3,3] | ||||
| B、[-2,2] | ||||
C、[
| ||||
D、[1-
|
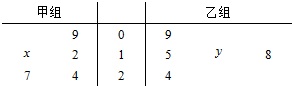 以下茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).
以下茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).