题目内容
19.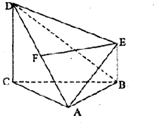 如图,四棱锥A-BCDE中,F为AD的中点,DC⊥平面ABC,CD∥BE,AB=AC=BC=CD=2BE.
如图,四棱锥A-BCDE中,F为AD的中点,DC⊥平面ABC,CD∥BE,AB=AC=BC=CD=2BE.(1)求证:EF⊥平面ACD;
(2)求平面ADE与平面ABD所成锐二面角的余弦值.
分析 (1)取AC中点O,连结BO、FO,推导出EF⊥OF,EF⊥AC,由此能证明EF⊥平面ACD.
(2)以O为原点,OA为x轴,OB为y轴,OF为z轴,建立空间直角坐标系,利用向量法能求出平面ADE与平面ABD所成锐二面角的余弦值.
解答 证明:(1)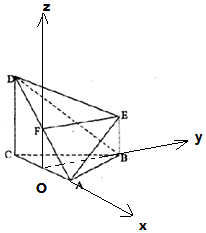 取AC中点O,连结BO、FO,
取AC中点O,连结BO、FO,
∵四棱锥A-BCDE中,F为AD的中点,DC⊥平面ABC,
CD∥BE,AB=AC=BC=CD=2BE,
∴OF$\underset{∥}{=}$BE,BE⊥OB,∴四边形CBEF是矩形,
∴EF⊥OF,EF⊥AC,
∵OF∩AC=O,∴EF⊥平面ACD.
解:(2)以O为原点,OA为x轴,OB为y轴,OF为z轴,建立空间直角坐标系,
设AB=AC=BC=CD=2BE=2,
则A(1,0,0),B(0,$\sqrt{3}$,0),D(-1,0,2),E(0,$\sqrt{3}$,1),
$\overrightarrow{AB}$=(-1,$\sqrt{3}$,0),$\overrightarrow{AD}$=(-2,0,2),$\overrightarrow{AE}$=(-1,$\sqrt{3},1$),
设平面ADE的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{AD}•\overrightarrow{n}=-2x+2z=0}\\{\overrightarrow{AE}•\overrightarrow{n}=-x+\sqrt{3}y+z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,0,1),
设平面ABD的法向量$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{AB}•\overrightarrow{m}=-a+\sqrt{3}b=0}\\{\overrightarrow{AD}•\overrightarrow{m}=-2a+2c=0}\end{array}\right.$,取a=$\sqrt{3}$,得$\overrightarrow{m}$=($\sqrt{3},1,\sqrt{3}$),
设平面ADE与平面ABD所成锐二面角为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{2\sqrt{3}}{\sqrt{2}•\sqrt{5}}$=$\frac{\sqrt{30}}{5}$.
∴平面ADE与平面ABD所成锐二面角的余弦值为$\frac{\sqrt{30}}{5}$.
点评 本题考查线面垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案(1)当n=1时,$\sqrt{{1}^{2}+1}$<1+1,不等式成立;
(2)假设当n=k(k∈N*)时不等式成立,即$\sqrt{{k}^{2}+1}$<k+1,则当n=k+1时,$\sqrt{(k+1)^{2}+1}$=$\sqrt{{k}^{2}+2k+2}$$<\sqrt{{k}^{2}+2k+2+2k+2}$=$\sqrt{(k+2)^{2}}$=(k+1)+1;所以当n=k+1时,不等式$\sqrt{{n}^{2}+1}$<n+1成立.
上述证明中( )
| A. | n=1验证不正确 | B. | 归纳假设不正确 | ||
| C. | 从n=k到n=k+1的推理不正确 | D. | 证明过程完全正确 |
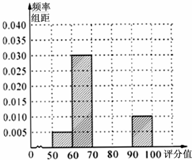 某单位进行了主题为“你幸福吗”的幸福指数问卷调查,得到每个调查对象的幸福指数评分值(百分制).现从收到的调查表中随机抽取20份进行统计,得到如图所示的频率分布表和频率分布直方图.
某单位进行了主题为“你幸福吗”的幸福指数问卷调查,得到每个调查对象的幸福指数评分值(百分制).现从收到的调查表中随机抽取20份进行统计,得到如图所示的频率分布表和频率分布直方图.(Ⅰ)请完成题目中的频率分布表,并补全题目中的频率分布直方图;
(Ⅱ)该单位将随机邀请被问卷调查的部分员工参加“幸福教育”的座谈会.在抽样统计的这20人中,已知幸福指数评分值在区间(80,100]的5人中有2人被邀请参加座谈,求其中幸福指数评分值在区间(80,90]的仅有1人被邀请的概率.
| 幸福指数评分值 | 频数 | 频率 |
| [50,60] | ||
| (60,70] | ||
| (70,80] | ||
| (80,90] | 3 | |
| (90,100] | ||
| 合 计 | 20 | 1 |

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | $\frac{1}{9}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{12}$ |
| A. | x=$\frac{7π}{12}$ | B. | x=$\frac{π}{2}$ | C. | x=$\frac{5π}{12}$ | D. | $x=\frac{π}{3}$ |
 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,PA⊥面ABCD,若PA=AB=BC=$\frac{1}{2}$AD.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,PA⊥面ABCD,若PA=AB=BC=$\frac{1}{2}$AD.