��Ŀ����
10�����ڲ���ʽ$\sqrt{{n}^{2}+1}$��n+1��n��N*����ijѧ������ѧ���ɷ�֤�����£���1����n=1ʱ��$\sqrt{{1}^{2}+1}$��1+1������ʽ������
��2�����赱n=k��k��N*��ʱ����ʽ��������$\sqrt{{k}^{2}+1}$��k+1����n=k+1ʱ��$\sqrt{��k+1��^{2}+1}$=$\sqrt{{k}^{2}+2k+2}$$��\sqrt{{k}^{2}+2k+2+2k+2}$=$\sqrt{��k+2��^{2}}$=��k+1��+1�����Ե�n=k+1ʱ������ʽ$\sqrt{{n}^{2}+1}$��n+1������
����֤���У�������
| A�� | n=1��֤����ȷ | B�� | ���ɼ��費��ȷ | ||
| C�� | ��n=k��n=k+1����������ȷ | D�� | ֤��������ȫ��ȷ |
���� ����ѧ���ɷ�֤������IJ����ǣ���һ������֤��n=n0ʱ����������ڶ������赱n=kʱ�����������ô��֤����n=k+1ʱ����Ҳ�������ؼ��ǵڶ�����Ҫ������Ϲ��ɼ���Ľ���
��� �⣺��n=1ʱ�����=$\sqrt{{1}^{2}+1}$=2���ұ�=1+1=2���ʵ�n=1ʱ������ʽ������
���赱n=k��k��N*��ʱ����ʽ��������$\sqrt{{k}^{2}+1}$��k+1����k2+1����k+1��2��
��n=k+1ʱ��$\sqrt{��k+1��^{2}+1}$=$\sqrt{{k}^{2}+2k+2}$��$\sqrt{��k+1��^{2}+2k+1}$=$\sqrt{��k+1��^{2}+2��k+1��+1-2}$=$\sqrt{��k+2��^{2}-2}$��$\sqrt{��k+2��^{2}}$=k+2=��k+1��+1��
�ʵ�n=k+1ʱ������ʽ������
��������������ʽ$\sqrt{{n}^{2}+1}$��n+1��n��N*����
�ɴ˿����жϴ�n=k��n=k+1����������ȷ�������ǣ�û�����ϼ��裬
��ѡ��C
���� ���⿼����ѧ���ɷ���˼�룬Ӧ����Ҫע��������Ϲ��ɼ���Ľ��ۣ�����ᵼ�´��������е��⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
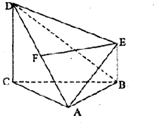 ��ͼ������A-BCDE�У�FΪAD���е㣬DC��ƽ��ABC��CD��BE��AB=AC=BC=CD=2BE��
��ͼ������A-BCDE�У�FΪAD���е㣬DC��ƽ��ABC��CD��BE��AB=AC=BC=CD=2BE��