题目内容
11.在极坐标系Ox中,曲线C1的方程为ρ=2sinθ,C2的方程为ρ=8sinθ,射线θ=$\frac{π}{3}$与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.分析 直接代入 θ=$\frac{π}{3}$求出A,B对应的ρ的值,两者之差即为线段AB的长.
解答 解:射线θ=$\frac{π}{3}$,A点的极径ρ1=4sin$\frac{π}{3}$=2$\sqrt{3}$,B点的极径ρ2=8sin$\frac{π}{3}$=4$\sqrt{3}$,
|AB|=|ρ2-ρ1|=4$\sqrt{3}$-2$\sqrt{3}$=2$\sqrt{3}$,
∴|AB|=2$\sqrt{3}$.
点评 本题考查极坐标方程的应用,极径的意义及求解,考查计算能力,转化思想的应用,属于基础题.

练习册系列答案
相关题目
1.若函数f(x)=2sin($\frac{π}{3}+\frac{π}{6}$)(-$\frac{1}{2}<x<\frac{11}{2}$)的图象与x轴交于点A,过A的直线l与函数f(x)的图象交于B,C两点,则($\overrightarrow{OB}+\overrightarrow{OC}$)$•\overrightarrow{OA}$=( )
| A. | 25 | B. | -$\frac{25}{2}$ | C. | $\frac{25}{2}$ | D. | -25 |
6.如图所示,AB=AC=1,DC=2BD,DE=EA,cos∠BAC=$\frac{1}{3}$,则BE=( )
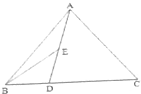

| A. | $\frac{59}{108}$ | B. | $\frac{43}{108}$ | C. | $\frac{\sqrt{177}}{18}$ | D. | $\frac{\sqrt{129}}{18}$ |
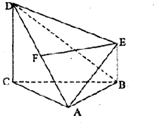 如图,四棱锥A-BCDE中,F为AD的中点,DC⊥平面ABC,CD∥BE,AB=AC=BC=CD=2BE.
如图,四棱锥A-BCDE中,F为AD的中点,DC⊥平面ABC,CD∥BE,AB=AC=BC=CD=2BE.