题目内容
20.设函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x,0<x<9}\\{\frac{9}{x}+1,x≥9}\end{array}\right.$,若f(a)=f(b)=c(a≠b),且f′(a)<0(f′(x)为函数f(x)的导数),则a,b,c的大小关系是( )| A. | c<a<b | B. | a<b<c | C. | c<b<a | D. | b<c<a |
分析 作出函数f(x)的图象,求出导数,判断可得a>9,1<b<9,0<c<2,求出b=3c,b-c=3c-c,0<c<2,由g(c)=3c-c,0<c<2,求出导数,判断单调性,可得b>c,即可得到所求大小关系.
解答 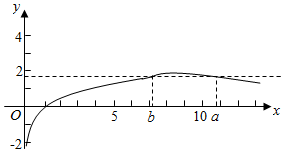 解:作出函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x,0<x<9}\\{\frac{9}{x}+1,x≥9}\end{array}\right.$的图象,
解:作出函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x,0<x<9}\\{\frac{9}{x}+1,x≥9}\end{array}\right.$的图象,
由f′(x)=$\left\{\begin{array}{l}{\frac{1}{xln3},0<x<9}\\{-\frac{9}{{x}^{2}},x≥9}\end{array}\right.$,
可得1<b<9,a>9,
log3b=$\frac{9}{a}$+1=c,
可得0<c<2,
b=3c,b-c=3c-c,0<c<2,
由g(c)=3c-c,0<c<2,
g′(c)=3cln3-1>0,
g(c)在(0,2)递增,可得g(c)>g(0)=1>0,
即有b>c,
即a>b>c.
故选:C.
点评 本题考查分段函数的应用:比较自变量的大小,注意运用数形结合的思想方法和构造函数,运用单调性,考查判断能力和分析问题的能力,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
15.已知集合A={x||2x-1|<3},B={x|x<1,或x>3},则A∩B等于( )
| A. | {x|-1<x<3} | B. | {x|x<2,或x>3} | C. | {x|-1<x<1} | D. | {x|x<-1,或x>3} |
5.如图,一个三棱锥的三视图均为直角三角形.若该三棱锥的顶点都在同一个球面上,则该球的表面积为( )


| A. | 4π | B. | 16π | C. | 24π | D. | 25π |
12. 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有30人,则n的值为
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有30人,则n的值为
( )
 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有30人,则n的值为
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有30人,则n的值为( )
| A. | 300 | B. | 200 | C. | 150 | D. | 100 |