题目内容
给定命题p:?x∈{x|x是无理数},x2是无理数;命题q:已知非零向量
、
,则“
⊥
”是“|
-
|=|
+
|”的充要条件.则下列各命题中,假命题是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、p∨q |
| B、(?p)∨q |
| C、(?p)∧q |
| D、(?p)∧(?q) |
考点:复合命题的真假
专题:简易逻辑
分析:由题意,要判断出两个命题p、q的真假,再由复合命题的判断规则找出四个选项中的假命题即可
解答:
解:命题p:?x∈{x|x是无理数},x2是无理数,不一定对,比如当x=
时,就不成立,故p假;
命题q:已知非零向量
、
,则“
⊥
”是“|
-
|=|
+
|”的充要条件是真命题,当“
⊥
”时,
•
=0,由于|
-
|2=
2+
2=|
+
|2,故可得|
-
|=|
+
|,充分性成立,反之,当|
-
|=|
+
|,必有|
-
|2=|
+
|2,展开得
•
=0,即
⊥
,必要性成立,故q:已知非零向量
、
,则“
⊥
”是“|
-
|=|
+
|”的充要条件是真命题
所以p∨q真,(?p)∨q真,(?p)∧q真,(?p)∧(?q)假,
故选D
| 2 |
命题q:已知非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
所以p∨q真,(?p)∨q真,(?p)∧q真,(?p)∧(?q)假,
故选D
点评:本题考查复合命题的真假判断,熟练掌握命题真假判断的规则是解答的关键,此类题常涉及到其它的知识,综合性较强

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
设全集I=R,M={x|x2>4},N={x|1<x<3},则(CIM)∩N为( )
| A、{x|x<2} |
| B、{x|1<x≤2} |
| C、{x|-2≤x<1} |
| D、{x|-2≤x≤2} |
已知函数f(x)=cos(2x+
)-cos2x,其中x∈R,给出下列四个结论
①函数f(x)是最小正周期为π的奇函数;
②函数f(x)图象的一条对称轴是x=
③函数f(x)图象的一个对称中心为(
,0)
④函数f(x)的递增区间为[kπ+
,kπ+
],k∈Z.
则正确结论的个数是( )
| π |
| 3 |
①函数f(x)是最小正周期为π的奇函数;
②函数f(x)图象的一条对称轴是x=
| 2π |
| 3 |
③函数f(x)图象的一个对称中心为(
| 5π |
| 12 |
④函数f(x)的递增区间为[kπ+
| π |
| 6 |
| 2π |
| 3 |
则正确结论的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知向量
=(2,1),
+
=(1,k2-1),则k=2是
⊥
的( )
| a |
| a |
| b |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知条件p:a=2,条件q:圆C1:x2+y2=9与圆C2:(x-a)2+y2=1相切,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
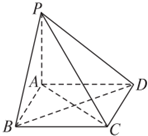 已知PA垂直于正方形ABCD所在平面,连接PB、PC、PD、AC、BD,则下列垂直关系中正确的序号是
已知PA垂直于正方形ABCD所在平面,连接PB、PC、PD、AC、BD,则下列垂直关系中正确的序号是