题目内容
3.若函数f(x)=sin2x+asinx+b(a,b∈R)在[-$\frac{π}{2}$,0]上存在零点,且0≤b-2a≤1,则b的取值范围是( )| A. | [-$\frac{2}{3}$,0] | B. | [-3,-2] | C. | [-2,0] | D. | [-3,0] |
分析 讨论零点个数,列出不等式组,作出平面区域,得出b的取值范围.
解答 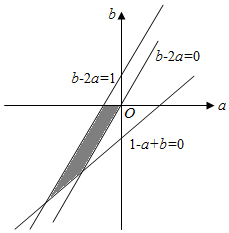 解:设sinx=t,则t∈[-1,0],
解:设sinx=t,则t∈[-1,0],
∴关于t的方程t2+at+b=0在[-1,0]上有解,
令g(t)=t2+at+b,
(1)若g(t)在[-1,0]上存在两个零点,则$\left\{\begin{array}{l}{b≥0}\\{1-a+b≥0}\\{{a}^{2}-4b>0}\\{-1<-\frac{a}{2}<0}\\{0≤b-2a≤1}\end{array}\right.$,无对应的平面区域,
(2)若g(t)在[-1,0]上存在1个零点,则g(-1)g(0)≤0,
∴$\left\{\begin{array}{l}{b(1-a+b)≤0}\\{0≤b-2a≤1}\end{array}\right.$,
作出平面区域如图所示:
解方程组$\left\{\begin{array}{l}{b-2a=1}\\{1-a+b=0}\end{array}\right.$得A(-2,-3).
∴b的范围是[-3,0].
故选D.
点评 本题考查了函数零点的存在性定理,简单的线性规划,属于中档题.

练习册系列答案
相关题目
13.已知椭圆x2+4y2=16的离心率等于( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
11.已知$A=\left\{{1,2,3,4,5,6,7,8}\right\},B=\left\{{x|x∈A且\sqrt{x}∈A}\right\}$,则B中的元素的个数为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
8.函数f(x)=|x-2|-kx+1有两个零点,则实数k的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | (1,2) | C. | (2,+∞) | D. | ($\frac{1}{2}$,1) |
12.过点A(2,3)和点B(2,-3)的直线方程是( )
| A. | x+2=0 | B. | x-2=0 | C. | y+2=0 | D. | y-2=0 |