题目内容
13.已知sin2θ=m,若θ∈(0,$\frac{π}{4}$),则sinθ-cosθ=-$\sqrt{1-m}$,若θ∈($\frac{π}{4}$,$\frac{π}{2}$),则sinθ-cosθ=$\sqrt{1-m}$.分析 若θ∈(0,$\frac{π}{4}$),则sinθ-cosθ<0,由sinθ-cosθ=-$\sqrt{(sinθ-cosθ)^{2}}$,利用已知及同角三角函数基本关系式,二倍角公式即可求值;若θ∈($\frac{π}{4}$,$\frac{π}{2}$),则sinθ-cosθ>0,同理计算求值即可.
解答 解:∵若θ∈(0,$\frac{π}{4}$),则sinθ-cosθ<0,
∴sinθ-cosθ=-$\sqrt{(sinθ-cosθ)^{2}}$=-$\sqrt{1-sin2θ}$=-$\sqrt{1-m}$;
∵若θ∈($\frac{π}{4}$,$\frac{π}{2}$),则sinθ-cosθ>0,
∴sinθ-cosθ=$\sqrt{(sinθ-cosθ)^{2}}$=$\sqrt{1-sin2θ}$=$\sqrt{1-m}$.
故答案为:-$\sqrt{1-m}$,$\sqrt{1-m}$.
点评 本题主要考查了正弦函数,余弦函数的图象和性质,考查了同角三角函数基本关系式,二倍角公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.在△ABC中,角A,B,C所对应的边长分别为a、b、c,若asinA+bsinB=2csinC,则cosC的最小值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
1.下列函数中,为偶函数的是( )
| A. | y=4x2-2 | B. | y=5x-7 | C. | y=x2(x>0) | D. | y=(x-1)2 |
8.函数y=$\frac{2}{{x}^{2}-9}$的定义域是( )
| A. | (-3,3) | B. | {-3,3} | C. | {x|x≠±3} | D. | (-∞,-3)∪(3,+∞) |
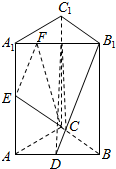 如图,在三棱柱ABC-A1B1C1中,D、E分别是AB、AA1的中点,AA1⊥平面ABC,AB⊥AC,AA1=4,AB=AC=2,且$\overrightarrow{{A}_{1}F}$=$\frac{1}{4}$$\overrightarrow{{A}_{1}{B}_{1}}$.
如图,在三棱柱ABC-A1B1C1中,D、E分别是AB、AA1的中点,AA1⊥平面ABC,AB⊥AC,AA1=4,AB=AC=2,且$\overrightarrow{{A}_{1}F}$=$\frac{1}{4}$$\overrightarrow{{A}_{1}{B}_{1}}$.