题目内容

设球的半径R=
3
cm，则此球的表面积为（　　）
A、36πcm2
B、12πcm2
C、4
3
πcm2
D、4πcm2
考点：球的体积和表面积
专题：空间位置关系与距离
分析：直接利用球的表面积公式，即可求得结论．
解答： 解：根据球的表面积公式可得S=4π×（
3
）2=12π．
故选：B．
点评：本题考查球的表面积公式，解题的关键是记清球的表面积公式．
练习册系列答案
相关题目
在△ABC中，已知AC=2，AB=4，∠A=60°，则BC=
 
．
如果全集U={1，2，3，4，5}，A={2，4}，B={1，3，4}，那么（∁UA）∪B=
 
．
设集合A={-1，2，3}，B={2a+4，a2+1}，A∩B={2}，则满足条件的实数a（　　）
A、只有一个B、有两个
C、有3个D、不存在
sin2（-30°）+sin2（67.5）°+2sin210°+tan405°的值是（　　）
A、
3+
2
4
B、
5+
2
4
C、
3-
2
4
D、
5-
2
4
已知函数f（x）=
x2(x≥0)
f(x+2)(x＜0)
，则f（-7）=（　　）
A、1B、4C、16D、49
一个小型家具厂计划生产A型和B型两种型号的桌子，每种类型桌子都要经过打磨、着色、上漆三道工序，A型桌子需要10min打磨，6min着色，6min上漆；B型桌子需要5min打磨，12min着色，9min上漆．如果一个工人每天打磨和上漆分别至多工作450min，着色每天至多工作480min，请你列出满足生产条件的数学关系式，并在直角坐标系中画出相应的平面区域．
制造甲、乙两种烟花，甲种烟花每枚含A药品3g、B药品4g、C药品4g，乙种烟花每枚含A药品2g、B药品11g、C药品6g．已知每天原料的使用限额为A药品120g、B药品400g、C药品240g，甲种烟花每枚可获利1.2美元，乙种烟花每枚可获利1美元，问每天应生产甲、乙两种烟花各多少枚才能获利最大？
已知函数f（x）是R上的可导函数，f（x）的导数f′（x）的图象如图，则下列结论正确的是（　　）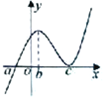
A、a，c分别是极大值点和极小值点
B、b，c分别是极大值点和极小值点
C、f（x）在区间（a，c）上是增函数
D、f（x）在区间（b，c）上是减函数

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网