题目内容
17.已知函数f(x)=x|x-a|+b,x∈R(1)判断f(x)的奇偶性;
(2)若a>0,函数 f(x)在区间[2,3]上为减函数,求实数a的取值范围.
分析 (1)讨论a=0,b=0时,a≠0或b≠0时,即可判断奇偶性;
(2)写出分段函数式,求得f(x)的减区间,由题意可得$\left\{\begin{array}{l}{\frac{a}{2}≤2}\\{a≥3}\end{array}\right.$,可得a的范围.
解答 解:(1)当a=0,b=0时,f(x)=x|x|为奇函数;
当a≠0或b≠0时,f(x)为非奇非偶函数.
(2)函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-ax+b,x≥a}\\{-{x}^{2}+ax+b,x<a}\end{array}\right.$,
当x≤a时,f(x)的递减区间为[$\frac{a}{2}$,a],
由题意可得$\left\{\begin{array}{l}{\frac{a}{2}≤2}\\{a≥3}\end{array}\right.$,
解得3≤a≤4.
点评 本题考查函数的奇偶性和单调性的判断和运用,考查运算能力,属于中档题.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
2.如图,已知PA垂直于平行四边形ABCD所在平面,若PC⊥BD,则平行四边形ABCD一定是( )
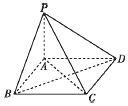

| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 非上述三种图形 |