题目内容
 如图,从地面上C,D两点望山顶A,测得它们的仰角分别为45°和30°,已知CD=100米,点C位于BD上,则山高AB等于( )
如图,从地面上C,D两点望山顶A,测得它们的仰角分别为45°和30°,已知CD=100米,点C位于BD上,则山高AB等于( )| A、100米 | ||
B、50
| ||
C、50
| ||
D、50(
|
考点:解三角形的实际应用
专题:应用题,解三角形
分析:设AB=xm,根据俯角的定义得到∠MAC=45°,∠MAD=30°,由平行线的性质得到∠D=30°,∠ACB=45°,再根据等腰三角形的性质得BC=AB=x,根据含30度的直角三角形三边的关系得DB=
AB,即100+x=
x,解出x即可.
| 3 |
| 3 |
解答:
解:设AB=xm,则由题意,∠D=30°,∠ACB=45°,
在Rt△ABC中,BC=AB=x,
在Rt△ADB中,DB=CD+BC=100+x,
∴DB=
AB,即100+x=
x,解得x=50(
+1)m.
∴山AB的高度为50(
+1)米.
故选:D.
在Rt△ABC中,BC=AB=x,
在Rt△ADB中,DB=CD+BC=100+x,
∴DB=
| 3 |
| 3 |
| 3 |
∴山AB的高度为50(
| 3 |
故选:D.
点评:此题考查了仰角的知识.要求学生能借助仰角构造直角三角形并解直角三角形,注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目
根据条件:a、b、c满足c<b<a,且a+b+c=0,有如下推理:
(1)ac(a-c)>0
(2)c(b-a)<0
(3)cb2≤ab2
(4)ab>ac
其中正确的是( )
(1)ac(a-c)>0
(2)c(b-a)<0
(3)cb2≤ab2
(4)ab>ac
其中正确的是( )
| A、(1)(2) |
| B、(3)(4) |
| C、(1)(3) |
| D、(2)(4) |
三棱锥P-ABC中中,顶点P中在底面ABC中内的射影为O中,若
(1)三条侧棱与底面所成的角相等,
(2)三条侧棱两两垂直,
(3)三个侧面与底面所成的角相等;
则点O中依次为垂心、内心、外心的条件分别是( )
(1)三条侧棱与底面所成的角相等,
(2)三条侧棱两两垂直,
(3)三个侧面与底面所成的角相等;
则点O中依次为垂心、内心、外心的条件分别是( )
| A、(1)(2)(3) |
| B、(3)(2)(1) |
| C、(2)(1)(3) |
| D、(2)(3)(1) |
已知某个几何体的三视图如图所示,根据图中数据,求这个几何体的体积是( )

A、
| ||
B、
| ||
C、
| ||
| D、2 |

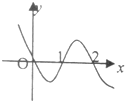
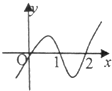
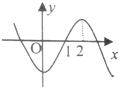
 函数y=f(x)的导函数f′(x)的图象如图所示,则y=f(x)的图象最有可能的是( )
函数y=f(x)的导函数f′(x)的图象如图所示,则y=f(x)的图象最有可能的是( )