题目内容
已知直线l:2x+y+2=0及圆C:x2+y2=2y.
(1)求垂直于直线l且与圆C相切的直线l′的方程;
(2)过直线l上的动点P作圆C的一条切线,设切点为T,求PT的最小值.
(1)求垂直于直线l且与圆C相切的直线l′的方程;
(2)过直线l上的动点P作圆C的一条切线,设切点为T,求PT的最小值.
考点:直线和圆的方程的应用
专题:直线与圆
分析:第(1)问由直线l′与直线l垂直可得其斜率,再利用待定系数法结合直线与圆相切的条件列出关于待定系数的方程求解;
第(2)问利用切线的性质,即切线长平方加上半径的平方等于P点到圆心距离的平方,从而把求PT的最小值转化为求动点P到圆心的距离的最小值,显然就是圆心到直线的距离最小.
第(2)问利用切线的性质,即切线长平方加上半径的平方等于P点到圆心距离的平方,从而把求PT的最小值转化为求动点P到圆心的距离的最小值,显然就是圆心到直线的距离最小.
解答:
解:∵l:2x+y+2=0及圆C:x2+y2=2y,即x2+(y-1)2=1,∴圆心C(0,1),r=1,
(1)∵l′⊥l,∴kl′=
,设l′的方程为 y=
x+b,即x-2y+2b=0,
则由l′与圆C相切得
=1,解得b=1±
,
所以切线方程为x-2y+2+
=0或x-2y+2-
=0.
(2)如图所示,设切点为T,P是直线上任一点,则由切线的性质可知PC2=PT2+1,所以要使PT最小,只需PC最小,则当PC⊥l时,PC最小,
此时PC表示C到直线l的距离,∴PC=
=
,PTmin=
=
.

(1)∵l′⊥l,∴kl′=
| 1 |
| 2 |
| 1 |
| 2 |
则由l′与圆C相切得
| |-2+2b| | ||
|
| ||
| 2 |
所以切线方程为x-2y+2+
| 5 |
| 5 |
(2)如图所示,设切点为T,P是直线上任一点,则由切线的性质可知PC2=PT2+1,所以要使PT最小,只需PC最小,则当PC⊥l时,PC最小,
此时PC表示C到直线l的距离,∴PC=
| |1+2| | ||
|
3
| ||
| 5 |
(
|
2
| ||
| 5 |

点评:直线与圆的位置关系,比如切线及切线长问题,弦长问题等的处理,一般用几何法即通过研究圆心到直线的距离、半径等的关系解决.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
执行如图所示的程序框图,则输出结果为( )


| A、初始输入中的a值 |
| B、三个数中的最大值 |
| C、三个数中的最小值 |
| D、初始输入中的c值 |
已知向量
=(-1,2),
=(10,5),则
与
( )
| a |
| b |
| a |
| b |
| A、垂直 | B、平行 |
| C、相交但不垂直 | D、无法判断 |
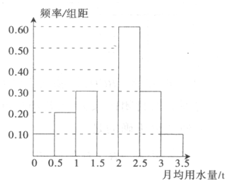 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准?用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准?用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,