Question

已知三棱柱P-ABC的各顶点都在以O为球心的球面上，且PA、PB、PC两垂直，若PA=PB=PC=2，则球O的表面积为（　　）

• A、12π
• B、10π
• C、8π
• D、6π

Answer 1

考点：球的体积和表面积

专题：计算题,空间位置关系与距离

分析：设过A，B，C的截面圆的圆心为O′，半径为r，球心O到该截面的距离为d，利用PA，PB，PC两两垂直，O′为△ABC的中心，求出截面圆的半径，通过球的半径截面圆的半径球心与截面的距离，求出球的半径，即可求出球的表面积．

解答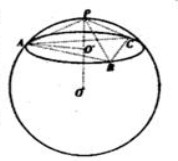： 解：如图，设过A，B，C的截面圆的圆心为O′，半径为r，球心O到该截面的距离为d，
因为PA，PB，PC两两垂直，且PA=PB=PC=2，∴AB=BC=CA=2

2

，且O′为△ABC的中心，
于是

2 2

sin60°

=2r，得r=

2 6

3

，
又PO′=

4-r2

=

2 3

3

．
OO′=R-

2 3

3

=d=

R2-r2

，解得R=

3

，
故S_球=4πR²=12π．
故选：A．

点评：本题是基础题，考查球的表面积的求法，球的截面圆的有关性质，考查空间想象能力，计算能力．