题目内容
以坐标原点O为极点,以x轴的非负半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρ-2cosθ=0,曲线C2的参数为
(t为参数).
(1)求曲线C1的参数方程;
(2)射线OM:θ=
与曲线C1的交点为O,P,与曲线C2交于点Q,求线段PQ的长.
|
(1)求曲线C1的参数方程;
(2)射线OM:θ=
| π |
| 3 |
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:(1)利用极坐标方程求出普通方程,然后利用三角代换求出曲线C1的参数方程.
(2)求出射线OM的方程,通过方程组求出P、Q坐标,然后利用两点间距离公式求解即可.
(2)求出射线OM的方程,通过方程组求出P、Q坐标,然后利用两点间距离公式求解即可.
解答:
解:(1)∵ρ-2cosθ=0,∴ρ2-2ρcosθ=0,∴x2+y2-2x=0,∴(x-1)2+y2=1
曲线C1的参数方程为
(θ为参数)
(2)射线OM:θ=
可得普通方程为:y=
x(x≥0).
,
∴3x2+x2-2x=0
∴P(
),
由
(t为参数),
∴y=-
x+3
,
,
∴Q(
,
),
PQ=
=2.
曲线C1的参数方程为
|
(2)射线OM:θ=
| π |
| 3 |
| 3 |
|
∴3x2+x2-2x=0
∴P(
| 1 |
| 2 |
| ||
| 2 |
由
|
∴y=-
| 3 |
| 3 |
|
∴Q(
| 3 |
| 2 |
3
| ||
| 2 |
PQ=
(
|
点评:本题考查极坐标与参数方程的应用,化为普通方程的方法,两点间距离公式的应用,考查计算能力.

练习册系列答案
相关题目
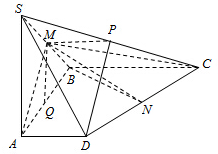 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA垂直底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1,M是棱SB的中点.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA垂直底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1,M是棱SB的中点.