题目内容
4.曲线y=$\frac{1}{4}{x^2}$在点(2,1)处的切线与x轴、y轴围成的封闭图形的面积为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
分析 先求出导数和切线的斜率,可得切线的方程,令x=0,y=0,求得在y轴的截距和在x轴的截距,由三角形的面积公式,计算即可得到所求值.
解答 解:y=$\frac{1}{4}$x2在(2,1)点处的切线l,
则y′=$\frac{1}{2}$x,
∴直线l的斜率k=y′|x=2=1,
∴直线l的方程为y-1=x-2,即y=x-1,
当y=0时,x-1=0,即x=1,
当x=0时,y=-1,
所围成的面积:S=$\frac{1}{2}$×1×1=$\frac{1}{2}$.
故选B.
点评 本题主要考查了导数的运用:求切线的方程,考查导数的几何意义,以及三角形的面积求法,正确求导和运用点斜式方程是解题的关键,属于基础题.

练习册系列答案
相关题目
13.将函数f(x)的图象向左平移$\frac{π}{6}$个单位后得到函数g(x)的图象如图所示,则函数f(x)的解析式是( )
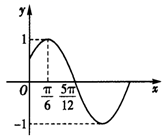

| A. | $f(x)=sin({2x-\frac{π}{6}})$(x∈R) | B. | $f(x)=sin({2x+\frac{π}{6}})$(x∈R) | C. | $f(x)=sin({2x-\frac{π}{3}})$(x∈R) | D. | $f(x)=sin({2x+\frac{π}{3}})$(x∈R) |
7.数列{an}满足a1=2,an+1=$\frac{2(n+2)}{n+1}$an(n∈N*),$\frac{{a}_{2017}}{{a}_{1}+{a}_{2}+…+{a}_{2016}}$=( )
| A. | $\frac{1009}{1008}$ | B. | $\frac{2015}{1007}$ | C. | $\frac{2016}{2015}$ | D. | $\frac{2015}{2014}$ |
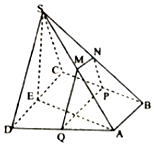 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=CD=SD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD的中点,过M,N作平面MNPQ分别与交BC,AD于点P,Q.
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=CD=SD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD的中点,过M,N作平面MNPQ分别与交BC,AD于点P,Q.