题目内容
2.若复数$\frac{a+3i}{1+2i}$(a∈R,i为虚数单位)是纯虚数,则实数a的值为( )| A. | -6 | B. | 13 | C. | $\frac{3}{2}$ | D. | $\sqrt{13}$ |
分析 利用复数代数形式的乘除运算化简,再由实部为0且虚部不为0列式求得a值.
解答 解:∵$\frac{a+3i}{1+2i}$=$\frac{(a+3i)(1-2i)}{(1+2i)(1-2i)}=\frac{a+6}{5}+\frac{3-2a}{5}i$是纯虚数,
∴$\left\{\begin{array}{l}{\frac{a+6}{5}=0}\\{\frac{3-2a}{5}≠0}\end{array}\right.$,解得a=-6.
故选:A.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
相关题目
13.将函数f(x)的图象向左平移$\frac{π}{6}$个单位后得到函数g(x)的图象如图所示,则函数f(x)的解析式是( )
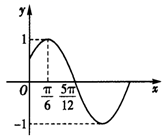

| A. | $f(x)=sin({2x-\frac{π}{6}})$(x∈R) | B. | $f(x)=sin({2x+\frac{π}{6}})$(x∈R) | C. | $f(x)=sin({2x-\frac{π}{3}})$(x∈R) | D. | $f(x)=sin({2x+\frac{π}{3}})$(x∈R) |
7.数列{an}满足a1=2,an+1=$\frac{2(n+2)}{n+1}$an(n∈N*),$\frac{{a}_{2017}}{{a}_{1}+{a}_{2}+…+{a}_{2016}}$=( )
| A. | $\frac{1009}{1008}$ | B. | $\frac{2015}{1007}$ | C. | $\frac{2016}{2015}$ | D. | $\frac{2015}{2014}$ |
5.已知集合A={x||x-1|<1},B={x|x2-1<0},则A∪B=( )
| A. | (-1,1) | B. | (-1,2) | C. | (1,2) | D. | (0,1) |