题目内容
已知f(x)=
是(-∞,+∞)上的减函数,那么a的取值范围( )
|
| A、(0,1) | ||||
B、(0,
| ||||
C、[
| ||||
D、[
|
考点:函数单调性的性质
专题:函数的性质及应用
分析:根据分段函数单调性的性质即可得到结论.
解答:
解:∵f(x)=
是(-∞,+∞)上的减函数,
∴满足
,
即
,
解得
≤a<
,
故选:C
|
∴满足
|
即
|
解得
| 1 |
| 4 |
| 1 |
| 2 |
故选:C
点评:本题主要考查函数的单调性的应用,根据复合函数单调性的性质是解决本题的关键.

练习册系列答案
相关题目
设f(x)=
,则f[f(ln2+1)]=( )
|
| A、log717 |
| B、2 |
| C、7 |
| D、log7(8e2+1) |
函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|≤
,x∈R)的部分图象如图所示,则该函数表达式为( )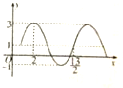
| π |
| 6 |

A、y=2sin(
| ||||
B、y=2sin(
| ||||
C、y=2sin(
| ||||
D、y=2sin(
|
等比数列{an}中,a4=4,则a2•a6等于( )
| A、4 | B、8 | C、16 | D、32 |
 如图,直线x=±π,y=±1围成的矩形区域内有一段余弦曲线y=-cosx,任意地向矩形投掷飞镖,则飞镖落入阴影区域的概率是
如图,直线x=±π,y=±1围成的矩形区域内有一段余弦曲线y=-cosx,任意地向矩形投掷飞镖,则飞镖落入阴影区域的概率是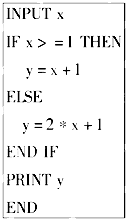 读程序,完成下列题目:程序如图:
读程序,完成下列题目:程序如图: