题目内容
1.已知数列{an}的前n项和为Sn,若4Sn=(2n-1)an+1+1,a1=1.(1)求数列{an}的通项公式;
(2)若数列{bn}满足$\frac{{b}_{n}}{{a}_{n}}$=($\sqrt{2}$)${\;}^{1+{a}_{n}}$,求数列{bn}的前n项和Tn.
分析 (1),两式相减可得an+1与an之间的递推关系,利用累加法,即可求出通项公式;
(2)bn=(2n-1)•${\sqrt{2}}^{2n}$=(2n-1)•2n,结合数列的项的特点考虑利用错位相减求和.
解答 解:(1)在4Sn=(2n-1)an+1+1中,令n=1,得a2=3,
∵4Sn=(2n-1)an+1+1,∴当n≥2时,4Sn-1=(2n-1)an+1,
两式相减,得:4an=(2n-1)an+1-(2n-3)an(n≥2)⇒$\frac{{{a_{n+1}}}}{a_n}=\frac{2n+1}{2n-1}(n≥2)$
${a_n}=\frac{a_n}{{{a_{n-1}}}}•\frac{{{a_{n-1}}}}{{{a_{n-2}}}}•\frac{{{a_{n-2}}}}{{{a_{n-3}}}}…\frac{a_3}{a_2}•\frac{a_2}{a_1}•{a_1}=\frac{2n-1}{2n-3}•\frac{2n-3}{2n-5}•\frac{2n-5}{2n-7}•…•\frac{5}{3}•\frac{3}{1}•1=2n-1$,
故an=2n-1;
(2)由(1)可得bn=(2n-1)•${\sqrt{2}}^{2n}$=(2n-1)•2n,
∴Tn=1×21+3×22+5×23+…+(2n-1)•2n,
∴2Tn=1×22+3×23+5×24+…+(2n-3)•2n+(2n-1)•2n+1,
∴-Tn=2+2(22+23+24+…+2n)-(2n-1)•2n+1
=2+2×$\frac{4(1-{2}^{n-1})}{1-2}$-(2n-1)•2n+1=-6-(2n-3)•2n+1,
∴Tn=(2n-3)•2n+1+6.
点评 本题主要考查了利用数列的递推公式,通项公式的应用及错位相减求和方法的应用,具有一定的综合性.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| A. | 9 | B. | 6 | C. | $2\sqrt{3}$ | D. | 3 |
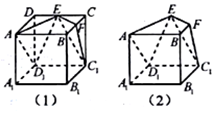 如图,在图(1)的正方体ABCD-A1B1C1D1中,E、F分别为CD、BC的中点,将图(1)中的正方体截去两个三棱锥,得到图(2)中的几何体,则该几何体的侧视图为( )
如图,在图(1)的正方体ABCD-A1B1C1D1中,E、F分别为CD、BC的中点,将图(1)中的正方体截去两个三棱锥,得到图(2)中的几何体,则该几何体的侧视图为( )