题目内容
10.已知A={x||3x-4|>2},$B=\left\{{\left.x\right|\frac{1}{{{x^2}-x-2}}>0}\right\}$,C={x|(x-a)(x-a-1)≥0},p:x∈∁RA,q:x∈∁RB,r:x∈C(1)p是q的什么条件?
(2)若r是p的必要非充分条件,试求实数a的取值范围.
分析 (1)分别求出p,q成立的x的范围,根据集合的包含关系以及充分必要条件的定义判断即可;
(2)解关于r的不等式,根据充分必要条件的定义得到关于a的不等式,解出即可.
解答 解:(1)由|3x-4|>2得3x-4>2或3x-4<-2,
即x>2或x<$\frac{2}{3}$,即p:$\frac{2}{3}$≤x≤2
由q:$\frac{1}{{x}^{2}-x-2}$>0得x2-x-2>0得x>2或x<-1,即q:-1≤x≤2,
则p是q的充分不必要条件.
(2)由(x-a)(x-a-1)≥0得x≤a或x≥a+1,即r:x≤a或x≥a+1,
若r是p的必要非充分条件,
即a≥2或a+1≤$\frac{2}{3}$,
即a≥2或a≤-$\frac{1}{3}$,
即实数a的取值范围是a≥2或a≤-$\frac{1}{3}$.
点评 本题考查了充分必要条件,考查集合的包含关系,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.设$f(x)=\sqrt{3}sinωx-cosωx(ω>0)$的最小正周期为π,则f(x)的一个单调递减区间是( )
| A. | $(-\frac{π}{2},0)$ | B. | $(-\frac{π}{6},\frac{π}{3})$ | C. | $(\frac{π}{3},\frac{5π}{6})$ | D. | $(\frac{π}{2},π)$ |
15.下列命题中,真命题是( )
| A. | 存在x∈R,ex≤0 | B. | a+b=0的充要条件是$\frac{a}{b}$=-1 | ||
| C. | 任意x∈R,2x>x2 | D. | a>1,b>1是ab>1的充分条件 |
19.如表是x,y的对应数据,由表中数据得线性回归方程为$\stackrel{∧}{y}$=0.8x-$\stackrel{∧}{a}$.那么,当x=60时,相应的$\stackrel{∧}{y}$为( )
| x | 15 | 20 | 25 | 30 | 35 |
| y | 6 | 12 | 14 | 20 | 23 |
| A. | 38 | B. | 43 | C. | 48 | D. | 52 |
20.已知角a的终边经过点P(-4,m),且$sinα=\frac{3}{5}$,则m等于( )
| A. | 3 | B. | $\frac{3}{5}$ | C. | -3 | D. | $-\frac{3}{5}$ |
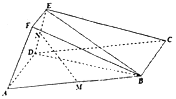 已知,平行四边形ABCD中,∠DAB=60°,AB=2AD=4EF=4ED=4,EF∥AD,AF=$\sqrt{2}$,M、N分别为线段AB、DE的中点
已知,平行四边形ABCD中,∠DAB=60°,AB=2AD=4EF=4ED=4,EF∥AD,AF=$\sqrt{2}$,M、N分别为线段AB、DE的中点