题目内容
9.已知函数f(x)=xm-$\frac{4}{x}$,且f(4)=3.(1)求m的值;
(2)求f(x)的奇偶性.
分析 (1)利用函数f(x)=xm-$\frac{4}{x}$,且f(4)=3,即可求m的值;
(2)利用奇函数的定义,即可求f(x)的奇偶性.
解答 解:(1)∵函数f(x)=xm-$\frac{4}{x}$,且f(4)=3,
∴4m-1=3,∴m=1;
(2)∵f(x)=x-$\frac{4}{x}$,
∴f(-x)=-x+$\frac{4}{x}$=-f(x),
∴f(x)是奇函数.
点评 本题考查奇函数的判断,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
4.已知等差数列{an}的公差d≠0,Sn为其前n项和,若a2,a3,a6成等比数列,且a10=-17,则$\frac{{S}_{n}}{{2}^{n}}$的最小值是( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{5}{8}$ | C. | $-\frac{3}{8}$ | D. | $-\frac{15}{32}$ |
14.已知△ABC的外接圆半径为1,圆心为点O,且$3\overrightarrow{OA}+4\overrightarrow{OB}+5\overrightarrow{OC}=0$,则$\overrightarrow{OC}•\overrightarrow{AB}$的值为( )
| A. | $\frac{8}{5}$ | B. | $\frac{7}{5}$ | C. | $-\frac{1}{5}$ | D. | $\frac{4}{5}$ |
18.设$f(x)=\sqrt{3}sinωx-cosωx(ω>0)$的最小正周期为π,则f(x)的一个单调递减区间是( )
| A. | $(-\frac{π}{2},0)$ | B. | $(-\frac{π}{6},\frac{π}{3})$ | C. | $(\frac{π}{3},\frac{5π}{6})$ | D. | $(\frac{π}{2},π)$ |
19.如表是x,y的对应数据,由表中数据得线性回归方程为$\stackrel{∧}{y}$=0.8x-$\stackrel{∧}{a}$.那么,当x=60时,相应的$\stackrel{∧}{y}$为( )
| x | 15 | 20 | 25 | 30 | 35 |
| y | 6 | 12 | 14 | 20 | 23 |
| A. | 38 | B. | 43 | C. | 48 | D. | 52 |
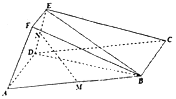 已知,平行四边形ABCD中,∠DAB=60°,AB=2AD=4EF=4ED=4,EF∥AD,AF=$\sqrt{2}$,M、N分别为线段AB、DE的中点
已知,平行四边形ABCD中,∠DAB=60°,AB=2AD=4EF=4ED=4,EF∥AD,AF=$\sqrt{2}$,M、N分别为线段AB、DE的中点