题目内容
6.已知实数x,y满足约束条件$\left\{\begin{array}{l}{2x-y-1≤0}\\{x-y+1≥0}\\{x≥0,y≥0}\end{array}\right.$,则z=2x+3y点的最大值是13.分析 画出约束条件的可行域,利用目标函数的几何意义求解最大值即可.
解答 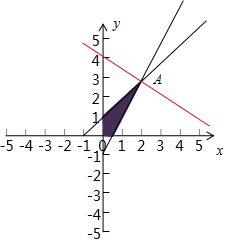 解:画出不等式组约束条件$\left\{\begin{array}{l}{2x-y-1≤0}\\{x-y+1≥0}\\{x≥0,y≥0}\end{array}\right.$,表示的平面区域如图所示,由$\left\{\begin{array}{l}{2x-y-1=0}\\{x-y+1=0}\end{array}\right.$,解得A(2,3).
解:画出不等式组约束条件$\left\{\begin{array}{l}{2x-y-1≤0}\\{x-y+1≥0}\\{x≥0,y≥0}\end{array}\right.$,表示的平面区域如图所示,由$\left\{\begin{array}{l}{2x-y-1=0}\\{x-y+1=0}\end{array}\right.$,解得A(2,3).
目标函数z=2x+3y的几何意义是直线y=-$\frac{2}{3}$x+$\frac{1}{3}z$在y轴上的截距的3倍,
易知目标函数在点A(2,3)处取得最大值,故z的最大值为:13.
故答案为:13.
点评 本题考查线性规划的简单应用,目标函数的最值的求法,考查转化思想以及计算能力.

练习册系列答案
相关题目
9.口袋中有100个大小相同的红球、白球、黑球,其中红球45个,从口袋中摸出一个球,摸出白球的概率为0.23,则摸出黑球的概率为( )
| A. | 0.32 | B. | 0.45 | C. | 0.64 | D. | 0.67 |
14.已知△ABC的外接圆半径为1,圆心为点O,且$3\overrightarrow{OA}+4\overrightarrow{OB}+5\overrightarrow{OC}=0$,则$\overrightarrow{OC}•\overrightarrow{AB}$的值为( )
| A. | $\frac{8}{5}$ | B. | $\frac{7}{5}$ | C. | $-\frac{1}{5}$ | D. | $\frac{4}{5}$ |
11.对于任意实数a,b,c,d以下四个命题中,其中正确的有( )
①ac2>bc2,则a>b,
②若a>b,c>d,则a+c>b+d;
③若a>b,c>d,则ac>bd;
④若a>b,则$\frac{1}{a}<\frac{1}{b}$.
①ac2>bc2,则a>b,
②若a>b,c>d,则a+c>b+d;
③若a>b,c>d,则ac>bd;
④若a>b,则$\frac{1}{a}<\frac{1}{b}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.设$f(x)=\sqrt{3}sinωx-cosωx(ω>0)$的最小正周期为π,则f(x)的一个单调递减区间是( )
| A. | $(-\frac{π}{2},0)$ | B. | $(-\frac{π}{6},\frac{π}{3})$ | C. | $(\frac{π}{3},\frac{5π}{6})$ | D. | $(\frac{π}{2},π)$ |
15.下列命题中,真命题是( )
| A. | 存在x∈R,ex≤0 | B. | a+b=0的充要条件是$\frac{a}{b}$=-1 | ||
| C. | 任意x∈R,2x>x2 | D. | a>1,b>1是ab>1的充分条件 |
16.已知x2+y 2=1,若x+y-k≥0对符合条件一切x、y都成立,则实数k的最大值为( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | 0 | D. | 1 |