题目内容
4．已知正四面体ABCD及其内切球O，经过该四面体的棱AD及底面ABC上的高DH作截面，交BC于点E，则截面图形正确的是（ ）| A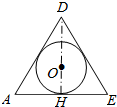． |  | B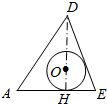． |  | C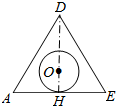． |  | D． |  |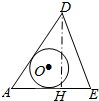
分析 根据题意，画出正四面体ABCD及其内切球O，作出截面ADE所表示的图形即可．
解答 解：画出图形，如图所示；
正四面体ABCD及其内切球O，经过该四面体的棱AD及底面ABC上的高DH作截面，交BC于点E，
则截面ADE所表示的图形是：
故选：B．
点评 本题考查了空间几何体与平面截面图的应用问题，也考查了空间想象能力的应用问题，是基础题目．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
14．“$?{x_0}∈{C_R}Q，x_0^2∈Q$”的否定是（ ）
| A． | $?{x_0}∉{C_R}Q，x_0^2∈Q$ | B． | $?{x_0}∈{C_R}Q，x_0^2∉Q$ | ||
| C． | $?{x_0}∈{C_R}Q，x_0^2∈Q$ | D． | $?{x_0}∈{C_R}Q，x_0^2∉Q$ |
15．已知集合A={x|2x≤4}，B={x|log2x＞0}，则A∩B=（ ）
| A． | [1，2] | B． | （1，2] | C． | （0，1） | D． | （0，1] |
12．已知α＞0且a≠1，函数f（x）=$\left\{\begin{array}{l}{（a-1）x+3a-4，（x≤0）}\\{{a}^{x}，（x＞0）}\end{array}\right.$满足对任意实数x1≠x2，都有x1f（x1）+x2f（x2）＞x1f（x2）+x2f（x1）成立，则a的取值范围是（ ）
| A． | $（1，\frac{5}{3}]$ | B． | （0，1） | C． | （1，+∞） | D． | $[\frac{5}{3}，2）$ |
19．在Rt△ABC中，∠ACB=90°，$sinA=\frac{{2\sqrt{5}}}{5}$，则tan2B等于（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $-\frac{4}{3}$ | D． | $-\frac{3}{4}$ |
9．函数f（x）=loga（ax-2）在[1，3]上单调递增，则a的取值范围是（ ）
| A． | （1，+∞） | B． | （0，2） | C． | （0，$\frac{2}{3}$） | D． | （2，+∞） |
13．集合A={x|y=log2（x+1）}，B={-1，0，1}，则A∩B等于（ ）
| A． | {0，1} | B． | {-1，0，1} | C． | {0} | D． | {1} |