题目内容
5.已知sinα=$\frac{3}{5}$,cosβ=-$\frac{12}{13}$,α∈(0,$\frac{π}{2}$),β∈($\frac{π}{2}$,π),求:sin(α+β),cos(α+β)分析 利用同角三角函数基本关系式求出cosα,sinβ,然后利用两角和的正弦函数以及余弦函数求解即可.
解答 解:sinα=$\frac{3}{5}$,α∈(0,$\frac{π}{2}$),cosα=$\frac{4}{5}$,
cosβ=-$\frac{12}{13}$,β∈($\frac{π}{2}$,π),sinβ=$\frac{5}{12}$,
sin(α+β)=sinαcosβ+cosαsinβ
=$\frac{3}{5}×(-\frac{12}{13})$+$\frac{4}{5}×\frac{5}{13}$
=$-\frac{16}{65}$,
cos(α+β)=cosαcosβ-sinαsinβ
=$\frac{4}{5}×(-\frac{12}{13})-\frac{3}{5}×\frac{5}{13}$
=-$\frac{63}{65}$.
点评 本题考查同角三角函数基本关系式以及两角和的正弦函数以及余弦函数的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在△ABC中,如果sinA:sinB:sinC=6:7:9,则△ABC一定是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 不能确定 |
17.已知$\vec a$=(-1,3),$\vec b$=(1,t),若($\vec a$-2$\vec b$)⊥$\vec a$,则|${\vec b}$|=( )
| A. | 5 | B. | $\sqrt{2}$ | C. | $\sqrt{10}$ | D. | $\sqrt{5}$ |
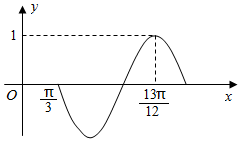 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.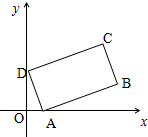 如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别位于x轴、y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}•\overrightarrow{OC}$的最大值是6.
如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别位于x轴、y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}•\overrightarrow{OC}$的最大值是6.