题目内容
2．以点P（3，4）和点Q（-5，6）为一条直径的两个端点的圆的方程是（x+1）2+（y-5）2=17．分析 由中点坐标公式求出圆心，由两点间距离公式求出圆半径，由此能求出圆的方程．
解答 解：∵点P（3，4）和点Q（-5，6），
∴以点P（3，4）和点Q（-5，6）为一条直径的两个端点的圆的圆心为（-1，5），
圆的半径r=$\frac{1}{2}|PQ|$=$\frac{1}{2}\sqrt{（3+5）^{2}+（4-6）^{2}}$=$\sqrt{17}$．
∴圆的方程为：（x+1）2+（y-5）2=17．
故答案为：（x+1）2+（y-5）2=17．
点评 本题考查圆的方程的求法，是基础题，解题时要认真审题，注意中点坐标公式和两点间距离公式的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
13．函数f（x）=cosx的一个单调递增区间是（ ）
| A． | （0，$\frac{π}{2}$） | B． | （-$\frac{π}{2}$，$\frac{π}{2}$） | C． | （-π，0） | D． | （0，π） |
14．
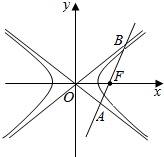如图，双曲线的中心在坐标原点O，焦点在x轴上，两条渐近线分别为11，12，经过右焦点F垂直于11的直线分别交11，12于A，B两点，若|$\overrightarrow{OA}$|，|$\overrightarrow{AB}$|，|$\overrightarrow{OB}$|依次成等差数列，则该双曲线的离心率为（ ）
如图，双曲线的中心在坐标原点O，焦点在x轴上，两条渐近线分别为11，12，经过右焦点F垂直于11的直线分别交11，12于A，B两点，若|$\overrightarrow{OA}$|，|$\overrightarrow{AB}$|，|$\overrightarrow{OB}$|依次成等差数列，则该双曲线的离心率为（ ）| A． | $\frac{\sqrt{5}}{2}$ | B． | $\sqrt{2}$ | C． | 2 | D． | $\sqrt{5}$ |