题目内容
14.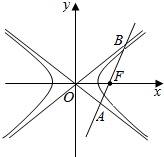 如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为11,12,经过右焦点F垂直于11的直线分别交11,12于A,B两点,若|$\overrightarrow{OA}$|,|$\overrightarrow{AB}$|,|$\overrightarrow{OB}$|依次成等差数列,则该双曲线的离心率为( )
如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为11,12,经过右焦点F垂直于11的直线分别交11,12于A,B两点,若|$\overrightarrow{OA}$|,|$\overrightarrow{AB}$|,|$\overrightarrow{OB}$|依次成等差数列,则该双曲线的离心率为( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
分析 由勾股定理得出直角三角形的2个直角边的长度比,联想到渐近线的夹角,求出渐近线的斜率,即可求出离心率.
解答 解:由题意,∵|$\overrightarrow{OA}$|,|$\overrightarrow{AB}$|,|$\overrightarrow{OB}$|依次成等差数列,
∴2|AB|=|OB|+|OA|,
∵|AB|2=(|OB|-|OA|)(|OB|+|OA|)=(|OB|-|OA|)2|AB|
∴|AB|=2(|OB|-|OA|),
∵2|AB|=|OB|+|OA|
∴|OA|=$\frac{3}{4}$|AB|,
∴tan∠AOB=$\frac{4}{3}$
而由对称性可知:OA的斜率为k=tan($\frac{π}{2}$-$\frac{1}{2}$∠AOB)
∴$\frac{2k}{1-{k}^{2}}$=$\frac{4}{3}$,∴2k2+3k-2=0,∴k=$\frac{1}{2}$(k=-2舍去);
∴$\frac{b}{a}$=$\frac{1}{2}$,∴a=2b,
∴c=$\sqrt{5}$b
∴e=$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$.
故选:A.
点评 本题考查了双曲线的简单性质以及等差数列的性质,由|OA|=$\frac{3}{4}$|AB|,联想到对应的是渐近线的夹角的正切值,是解题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
19.定义在R上的函数f(x)满足f(x+2)=$\frac{1}{2}$f(x),当x∈[0,2)时,f(x)=$\left\{\begin{array}{l}{\frac{1}{2}-2{x}^{2},0≤x<1}\\{-{2}^{1-|x-\frac{3}{2}|},1≤x<2}\end{array}\right.$,函数g(x)=(2x-x2)ex+m,若?x1∈[-4,-2),?x2∈[-1,2],使得不等式f(x1)-g(x2)≥0成立,则实数m的取值范围是( )
| A. | (-∞,-8] | B. | (-∞,$\frac{3}{e}$+8] | C. | [$\frac{3}{e}$-8,+∞) | D. | (-∞,$\frac{3}{e}$-8] |
 如图,四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,且PD=AB=2.
如图,四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,且PD=AB=2.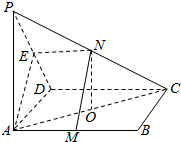 如图,己知P是平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点,E是PD的中点,O是AC的中点.
如图,己知P是平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点,E是PD的中点,O是AC的中点.