题目内容
16.已知数列{an}满足an+1=an+1(n∈N*),且a1=1,则$\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_{99}}{a_{100}}}}$=$\frac{99}{100}$.分析 利用裂项消项法,求解数列的和即可.
解答 解:数列{an}满足an+1=an+1(n∈N*),且a1=1,数列是等差数列,an=n.
则$\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_{99}}{a_{100}}}}$=$\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{99}-\frac{1}{100}$=1-$\frac{1}{100}$=$\frac{99}{100}$.
故答案为:$\frac{99}{100}$.
点评 本题考查等差数列的应用,数列求和,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.如图,在正三棱柱ABC-A1B1C1中,$AB=\sqrt{2}B{B_1}$,则AB1与C1B所成角的大小为( )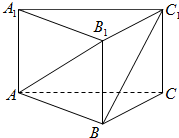

| A. | 45° | B. | 60° | C. | 90° | D. | 105° |
11.命题“若a>2,则a>1”及其逆命题、否命题、逆否命题这四个命题中,真命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
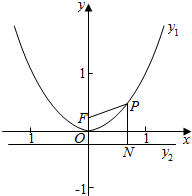 如图所示,在平面直角坐际系中有一抛物线y1=ax2,且抛物线经过点(2a-1,1),y轴上有一定点F,其坐标为(0,$\frac{1}{4}$),直线1的解析式为y2=-$\frac{1}{4}$,在抛物线上有一动点P,连接PF,并过点P作PN⊥直线1.
如图所示,在平面直角坐际系中有一抛物线y1=ax2,且抛物线经过点(2a-1,1),y轴上有一定点F,其坐标为(0,$\frac{1}{4}$),直线1的解析式为y2=-$\frac{1}{4}$,在抛物线上有一动点P,连接PF,并过点P作PN⊥直线1.