题目内容
7.在正方体ABCD-A1B1C1D1中,点P、Q分别在A1B1、C1D1上,且A1P=2PB1,C1Q=2QD1,则异面直线BP与DQ所成角的余弦值为$\frac{4}{5}$.分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线BP与DQ所成角的余弦值.
解答 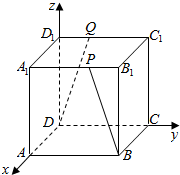 解:设正方体ABCD-A1B1C1D1中棱长为3,
解:设正方体ABCD-A1B1C1D1中棱长为3,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则D(0,0,0),Q(0,1,3),B(3,3,0),P(3,2,3),
$\overrightarrow{BP}$=(0,-1,3),$\overrightarrow{DQ}$=(0,1,3),
设异面直线BP与DQ所成角为θ,
则cosθ=$\frac{|\overrightarrow{BP}•\overrightarrow{DQ}|}{|\overrightarrow{BP}|•|\overrightarrow{DQ}|}$=$\frac{8}{\sqrt{10}•\sqrt{10}}$=$\frac{4}{5}$.
异面直线BP与DQ所成角的余弦值为$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
17.在下列向量组中,可以用它们作基底把向量$\overrightarrow{m}$=(-3,5)表示出来的是( )
| A. | $\overrightarrow{{e}_{1}}$=(-2,3),$\overrightarrow{{e}_{2}}$=(4,-6) | B. | $\overrightarrow{{e}_{1}}$=(1,5),$\overrightarrow{{e}_{2}}$=(-2,1) | ||
| C. | $\overrightarrow{{e}_{1}}$=(2,3),$\overrightarrow{{e}_{2}}$=(-1,-$\frac{3}{2}$) | D. | $\overrightarrow{{e}_{1}}$=(3,4),$\overrightarrow{{e}_{2}}$=(-6,-8) |
2.已知命题p:“若直线a与平面α内两条直线垂直,则直线a与平面α垂直”,命题q:“存在两个相交平面垂直于同一条直线”,则下列命题中的真命题为( )
| A. | p∧q | B. | p∨q | C. | ¬p∨q | D. | p∧¬q |
12.两条平行直线3x-4y+12=0与3x-4y-13=0间的距离为( )
| A. | $\frac{1}{5}$ | B. | $\frac{5}{2}$ | C. | $\frac{23}{5}$ | D. | 5 |
19.下列函数中,在其定义域内是偶函数为( )
| A. | $f(x)=\frac{1}{x}$ | B. | f(x)=2x | C. | f(x)=lgx | D. | f(x)=cosx |
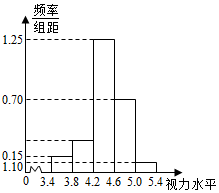 为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示).若在[5.0,5.4]内的学生人数是2,则根据图中数据可得被样本数据在[3.8,4.2)内的人数是6.
为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示).若在[5.0,5.4]内的学生人数是2,则根据图中数据可得被样本数据在[3.8,4.2)内的人数是6.